pdf Der folgende Text ist ein Versuch. Aus der Fachliteratur ist zwar bekannt, dass die hier angegangenen Probleme existieren. Was ich dazu schreibe, ist aber am Schreibtisch entstanden und noch nicht erprobt. Es ist daher noch unklar, ob die hier gewählte Darstellung für Berufsschullehrpersonen verständlich und nützlich ist. Für Rückmeldungen bin ich dankbar!

 Wie andere beim Rechnen bzw. in der Mathematik verwendeten Zeichen (Gleichheitszeichen und Bruchstriche) wird auch das Minuszeichen in mehreren verschiedenen Bedeutungen bzw. Funktionen eingesetzt. Dass die Lernenden daher manchmal verwirrt sind, ist verständlich. Man kann ihnen helfen, indem man sie dabei unterstützt, geeignete Vorstellungen für die verschiedenen Funktionen aufzubauen.

1     Drei Verwendungen des Minuszeichens

Es lassen sich mindestens die drei folgenden Verwendungen des Minuszeichens unterscheiden (Coutat & Dorier 2016):

1.1 Operation „Wegnehmen“: 5 – 3

Dies ist die ursprünglichste Verwendung des Minuszeichens und auch diejenige, welche man typischerweise als erste kennenlernt. Solange das Resultat der Operation grösser oder gleich Null ist, dürften die wenigsten Lernenden damit Schwierigkeiten haben.

1.2 Kennzeichen einer negativen Zahl: -3

„Unter null“ gerät man bspw. in der Buchhaltung, wenn man 3 Franken besitzt und 5 Franken ausgibt und nun 2 Franken Schulden hat – was man als „-2“ schreiben kann. Zumindest in Europa taten sich aber selbst die Mathematiker lange Zeit schwer, so etwas wie „-2“ als Zahl anzuerkennen. So schrieb bspw. D’Alembert (ein bekannter und geschätzter Mathematiker) noch 1784 in einem Artikel: „ … dass man die Grössen, die man negative nennt … fälschlich als unterhalb der Null gelegen ansieht“ (D’Alembert 1784, S. 73; mehr dazu im Anhang).

Und Kant meinte, dass zwar bspw. Schulden das Gegenteil, die Negation eines Guthabens sind, und dass 2 Franken Schulden 2 Franken Guthaben aufheben, so dass man sie auch verrechnen kann. Es sei aber absurd zu sagen, dass 2 Franken Schulden geschrieben als „-2“ weniger als 0 bzw. weniger als Nichts sei (Kant 1797). Dass negative Zahlen und positive Zahlen zwei verschiedene Sorten von Zahlen sind, die eigentlich beide „positiv“ zu verstehen sind, findet man heute noch, wenn in einer Buchhaltung Schulden durch rote Zahlen und ohne Minuszeichen dargestellt werden.

Erst im 19. Jahrhundert konnte sich die Vorstellung der Zahlengeraden etablieren, auf der man ausgehend von 0 nicht nur nach „rechts“ in Richtung immer grösserer Zahlen gelangt sondern auch nach „links“ in Richtung immer kleinerer Zahlen. Und erst dadurch wurden bspw. die Voraussetzungen für die Temperaturskala von Celsius geschaffen, bei der „-4 Grad“ tatsächlich weniger als „0 Grad“ sind und bei der sich „-4 Grad“ und „+4 Grad“ nicht in dem Sinn aufheben, wie sich Schulden und Guthaben aufheben. Damit hatte das Minuszeichen eine zweite Funktion erhalten als Kennzeichnung für Zahlen, die mehr oder weniger weit unter 0 liegen.

1.3 Negation:  -(-3) = (+3)

Hat man 6 Franken in bar aber auch noch 3 Franken Schulden, so besitzt man eigentlich nur 3 Franken. Kurz kann man das schreiben als 6 + (-3) = 3. Werden die 3 Franken Schulden irgendwie bezahlt, dann besitzt man wieder volle 6 Franken. Kurz: 3 -(-3) = 6 d.h. -(-3) hat denselben Effekt wie +3. Oder in den Worten Kants ausgedrückt: Die Negation von 3 Franken Schulden ist 3 Franken Guthaben – und umgekehrt. Beginnt man also mit negativen Zahlen zu rechnen, kann das Minuszeichen drittens als Negation verstanden werden. + (-3) hat den umgekehrten Effekt wie + (+3), -3 hat den umgekehrten Effekt wie +3.

Zusammengefasst lassen sich also folgende drei Verwendungszwecke des Minuszeichens unterschieden, die man auseinanderhalten muss und die oft bunt gemischt auftreten:

• Operation „Wegnehmen“: 5 – 3
• Vorzeichen negativer Zahlen: -3
• Negation: -(-3) = (+3)

2     Ein verbindende Vorstellung

Für viele Lernende ist der Punkt, an dem sie definitiv an die Grenzen ihres Verständnisses des Minuszeichens gelangen, bei Rechnungen zu „Minus mal Minus“ erreicht, also bspw. (-2) × (-3) = (+6). Hier kann das Minuszeichen definitiv nicht mehr mit der vertrauten Handlung des „Wegnehmens“ in Verbindung gebracht werden. Dadurch ist das, was geschieht, nicht fassbar. Und da man sich bei rechnerischen Operationen nur sicher fühlt, wenn man sie im wörtlichen Sinn erfassen, in die Hand nehmen kann, setzt eine grosse Unsicherheit ein (Lakoff & Núñez 200, Coutat & Dorier 2016).

Man kann den Lernenden helfen, alle drei Funktionen des Minuszeichens fassbar zu machen, indem man sie anhand der Zahlengeraden interpretiert.

2.1 Vorzeichen negativer Zahlen

Auf der Zahlengeraden ist eine Zahl ein Zählvorgang, der bei 0 beginnt und an einer bestimmten Stelle endet. 3 steht für: „Ich starte bei 0 und gehe Schritt um Schritt zählend 1,2,3“. Man kann das durch einen mehr oder weniger langen Pfeil ausgehend von 0 darstellen.

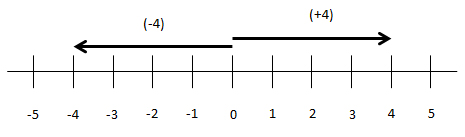
Das Minuszeichen bei (-4) signalisiert dann, dass ich nach links anstatt nach rechts starten soll.

2.2 Operation „Wegnehmen“

Im Bild der Zahlengerade ist eine Operation immer eine Anweisung, wie mehrere solche als Pfeile dargestellte Zählvorgänge zu verknüpfen sind. Das Minuszeichen bedeutet, dass man vom Punkt ausgehend, den man nach dem ersten Zählvorgang erreicht hat einen zweiten solchen Vorgang nach links hin starten soll. 4 – 3 meint so interpretiert also: Zähle zuerst 1,2,3,4 nach rechts und dann von dort aus 1,2,3 nach links.

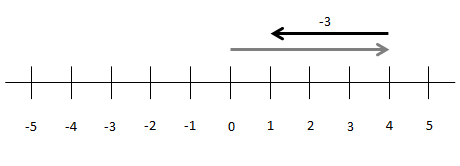
Umgekehrt steht das Pluszeichen bei 4+3 dafür, dass man nach rechts weiterzählt. Das Minuszeichen signalisiert also in dieser Funktion, dass man nach links weitermachen soll. So gesehen wird auch deutlich, warum sich die beiden Funktionen Vorzeichen und Operator vertragen, denn man kann das Vorzeichen auch einfach als Abkürzung für die Operation „Zähle zuerst nichts und zähle dann nach links“ verstehen.

2.3 Negation

Die durch das Minuszeichen dargestellte Negation ist auf der Zahlengeraden auch eine Operation. Sie ist aber nicht eine Anweisung, wie man weiterzählen soll, sondern wie man den beim ersten Zähvorgang entstandenen „Pfeil“ verändern soll. -(-3) kann man verstehen als: Zähle zuerst 1,2,3 nach links und drehe dann den Pfeil 180 Grad um den Nullpunkt.

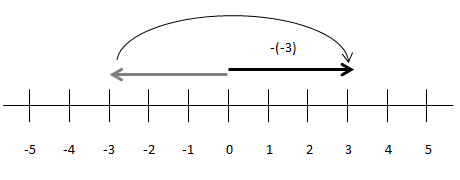
Ein Gegenstück zu dieser Drehung symbolisiert durch das Pluszeichen gibt es nicht. Auch wenn man einen Pfeil von rechts nach links drehen will, schreibt sich das mit Hilfe des Minuszeichens: -(+4) = (-4).

2.4 Warum gibt (-2) × (-3) sechs?

Damit sind alle drei Funktionen des Minuszeichens handgreiflich im Zählen und manipulieren auf der Zahlengerade verankert. Um die Multiplikation mit negativen Zahlen greifbar zu machen, muss allerdings zuerst auch noch die Multiplikation im Bild der Zahlengerade interpretiert werden.

Die Multiplikation ist hier eine Operation im gleichen Sinn wie die Negation. Sie gibt eine Anweisung, wie man den beim ersten Zählvorgang entstandenen „Pfeil“ verändern soll. (-2) × 3 kann man verstehen als: Zähle zuerst nach links 1,2 und strecke dann den Pfeil auf das Dreifache, also (-2) × 3 = (-6).

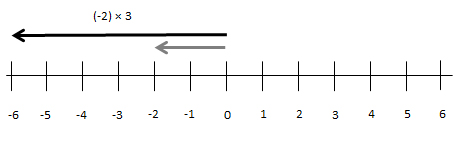
Die beiden Zahlen (-2) und 3 haben hier zwei verschiedene Funktionen. Die erste Zahl ist eine „abgezählte“ Zahl (dargestellt als Pfeil), die zweite ist als Streckungsfaktor Teil des Operators.

Und so wird deutlich wie man (-2) × -3 interpretieren muss: „mal -3“ ist ein komplexer Operator, zusammengesetzt aus einer Streckung (mal) und einer Drehung (minus in der Bedeutung Negation), also (-2) × -3 = (+6).

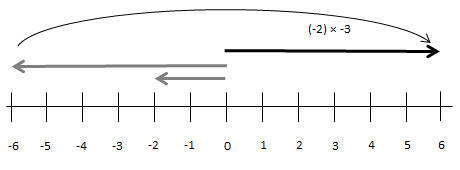
Deutlicher sichtbar würde das, wenn man -((-2) × 3) schreiben würde. Die übliche Notation (-2) × (-3) wird gewählt, da man die Rollen von (-2) und (-3) tauschen kann. Wenn wir (-3) als abgezählte Zahl interpretieren, diese dann auf das Doppelte strecken (×2) und anschliessend drehen (-), dann erhalten wir auch (+6). Das ist sehr elegant, führt aber dazu, dass in der schriftlichen Darstellung beim Operator „× (-3)“ die zusammengehörenden Teile der Multiplikation (×3) durch das Minuszeichen auseinander gerissen werden – was Verwirrungen eher fördert als mindert.

3     Erwähnte Literatur

• D’Alembert, Jean-Baptiste le Rond (1784). Négatif. In: Diderot & d’Alembert. Encyclopédie méthodique / Mathématiques. Tome 11, 72-74.
  [französisch, deutsche Übersetzung].
• Coutat, S., & Dorier, J.-L. (2016). Comment la corporéité peut-elle intervenir dans l’apprentissage des mathématiques? Quelques références et deux exemples. Schweiz. Zeitschrift für Bildungswissenschaften, 38(1), 23-37.
• Kant, I. (1797) Versuch den Begriff der negativen Grössen in die Weltweisheit einzuführen [Aus Immanuel Kant (1977). Werke in zwölf Bänden. Band 2, Frankfurt am Main, 783-791.]
• Lakoff, G., & Núñez, R. (2000). Where Mathematics Comes From: How the Embodied Mind Brings Mathematics into Being. New York: Basic Books.

4     Anhang: D’Alemberts Überlegung

Stellen wir uns beispielsweise vor, gesucht sei der Wert einer Zahl x, die zu 100 hinzugefügt wird, so dass es 50 macht, dann hat man nach den Regeln der Algebra x +100 = 50 und x = -50 , was zeigt, dass die Größe x gleich 50 ist, und dass sie, statt zu 100 hinzugefügt zu werden, abgezogen werden muss, so dass man das Problem so hätte formulieren müssen: zu finden ist eine Größe x, bei deren Abzug von 100 ein Rest von 50 bleibt; und wenn man das Problem so formulierte, hätte man 100 – x = 50 und x = 50 und die negative Form von x bestünde nicht mehr. So deuten die negativen Größen in der Rechnung in Wirklichkeit positive Größen an, aber solche, die man in einer falschen Position vermutet hat. (D’Alembert 1783, S. 73)