etwas ausfühlicher als pdf

Der folgende Text ist ein Versuch. Ich weiss, dass das hier angegangene Problem existiert, und ich bin mir auch ziemlich sicher, in welchen Kontexten „Bruchstriche“ vorkommen, d.h. für welche Kontexte Lehrpersonen in der Berufsbildung Unterstützung benötigen würden. Was ich dazu geschrieben habe, ist aber am Schreibtisch entstanden und noch nicht erprobt. Es ist daher noch unklar, ob die hier gewählte Darstellung für Berufsschullehrpersonen verständlich und nützlich ist und ob die vorgeschlagen Vorstellungen zu den einzelnen Kontexten für ihre Lernenden nützlich sind. Für Rückmeldungen zu beiden Punkten bin ich dankbar!

1 Widerstände

Angehende Elektromonteure müssen im ersten Lehrjahr Bruchterme wie die folgenden bearbeiten: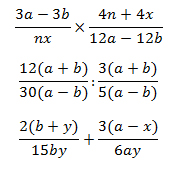

Warum das so ist, lässt sich nicht so leicht in Erfahrung bringen. Ein Grund dafür dürfte aber der Zusammenhang zwischen den Teilwiderständen und dem Gesamtwiderstand in einer Parallelschaltung sein:

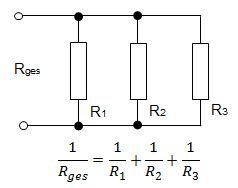
Diese Gleichung umgeformt und nach R_ges „aufgelöst“ ergibt folgenden Doppelbruch:

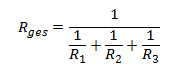
Sind es nur zwei Teilwiderständen, dann kann man, wenn man das nützlich findet, auch weiter umformen, bis man beispielsweise folgende Formeln erhält:

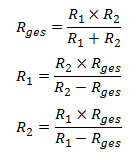
Und da für Elektromonteure im praktischen Alltag parallele Widerstände eine gewisse Rolle spielen, kann man daraus natürlich folgern, dass für sie komplexe Bruchterme von Bedeutung sind.

Allerdings ist es möglich, das Ganze auch anders anzugehen: 1/R, d.h. der Kehrwert des Widerstandes hat auch einen Namen. Er wird als „Leitwert“ bezeichnet und mit G abgekürzt: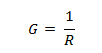

Der Zusammenhang zwischen G und R ist intuitiv leicht nachvollziehbar: Je grösser der Widerstand (R), umso kleiner der Leitwert (G), d.h. umso schlechter leitet das betrachtete elektronische Bauteil. Und umgekehrt: Je kleiner der Widerstand, umso grösser der Leitwert, d.h. umso besser leitet das Bauteil. Mit G an Stelle von 1/R wird der Zusammenhang von oben zu:

Auch das ist intuitiv nachvollziehbar: Wenn man parallel zu einem Bauteil mit dem Leitwert G₁ ein zweites Bauteil mit dem Leitwert G₂ einfügt, dann steigt der gesamte Leitwert von vorher G₁ um den Leitwert des neu dazugekommen Teils (G₂) auf G₁+G₂. Und rechnerisch ist es einfach, aus bekannten Leitwerten einen unbekannten abzuleiten, beispielsweise bei zwei Bauteilen:

Benötigt man dann nicht den Leitwert, sondern den Widerstand, kann man immer noch den Kehrwert nehmen. So betrachtet, gibt es keinen Grund, mit Elektromonteuren komplexe Bruchterme zu behandeln. Das einzige, was sie können müssen, ist mit Kehrwerten umgehen.

2 Bruchstriche und Brüche

Nicht immer, wenn ein Bruchstrich auftritt, handelt es dabei um einen Bruch im engeren Sinn. Mit „Bruch im engeren Sinn“ sind die Situationen gemeint, in denen man beispielsweise 3/4 zu Recht als Teil eines Ganzen interpretieren kann, also etwa „ein zu 3/4 gefüllter Krug“. In diesen Situationen gelten die Regeln und Vorgehensweisen des klassischen Bruchrechnens mit Gleichnamig-Machen etc. Beispielsweise: „Schüttete man zu einem zu 3/4 gefüllten Krug noch den Inhalt eines zu 1/8 gefüllten (gleich grossen!) Kruges, so ist der erste Krug nun zu 7/8 gefüllt.“

Es gibt aber verschiedenste andere Situationen, in denen Bruchstriche andere Interpretationen haben (vgl. etwa Malle, 2004) und bei denen manchmal sogar die Regeln des klassischen Bruchrechnens nicht gelten. Soweit ich sehe, spielen dabei im beruflichen Kontext vor allem die folgenden vier eine Rolle:

• Kehrwerte: Widerstand = 1 / Leitwert
• Quotienten-Grössen: km/h, kg/m³, m³/ha
• Proportionen: Länge₁/Breite₁=Länge₂/Breite₂
• Innere Verhältnisse: Rote zu blaue Teile im Verhältnis 2/1

Dazu kommen noch Steigungsangaben, welche v.a. im Baugewerbe von Bedeutung sind und ebenfalls ihre eigenen Gesetzmässigkeiten haben.

2.1 Kehrwerte

Ein erstes Beispiel sind die Kehrwerte aus Abschnitt 1. 1/R beschreibt auf keine Art und Weise den Teil irgendeines „Ganzen“. Beim klassischen Bruchrechnen ist es äusserst wichtig, dass man weiss, auf welches „Ganze“ sich der Bruch bezieht. Die Rechnung oben funktioniert nur, wenn es sich beide Male um dasselbe „Ganze“ – hier konkret: gleich grosse Krüge – handelt (vgl. etwa Swanson & Williams, 2014; beim Prozentrechnen entspricht dies der Frage, worauf sich 100% bezieht.). Bei 1/R würde die Suche nach einem „Ganzen“ aber nur in die Irre führen.

1/R ist kein klassischer Bruch, sondern beschreibt die Beziehung zwischen zwei Grössen, dem Widerstand und dem Leitwert, von denen der eine auf eine bestimmte Art kleiner wird, wenn der andere grösser wird. Die Art dieses Zusammenhangs kann man graphisch so darstellen:

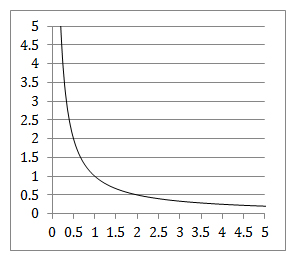
Wichtig ist hier also nicht die Vorstellung „Teil eines Ganzen“ (diese ist sogar irreführend), sondern wichtig sind Vorstellungen wie „Wenn ich den Widerstand verdopple, halbiert sich der Leitwert“. D.h.: Die relative Veränderung einer Grösse hat immer denselben Effekt auf die relative Veränderung der anderen Grösse. Wichtig ist daneben aber auch zu sehen, dass die absolute Veränderung einer Grösse nicht immer denselben Effekt hat: „Wenn ich die eine Grösse von 0.1 auf 0.2 erhöhe, sinkt die andere Grösse von 10 auf 5; wenn ich hingegen die eine Grösse von 1.0 auf 1.1 (also ebenfalls um 0.1) erhöhe, sinkt die andere Grösse nur um etwa 0.1 von 1 auf 0.9“.

2.2 Quotienten-Grössen

Bruchstriche treten im Weiteren bei Grössen auf, die als Verhältnis von zwei anderen Grössen angegeben werden: Geschwindigkeit (km/h), Dichte (kg/m³), Verbrauch (l/m²) etc. Auch hier wäre die Vorstellung „Teil eines Ganzen“ fehl am Platz. Wovon könnten 4 km/2 h „Teil“ sein?

Welche Vorstellungen hier wichtig sind und wo dabei Schwierigkeiten auftreten können, zeigt folgendes Beispiel: Agrarpraktiker werden angehalten, beim Düngen zumindest überschlagsmässig zu berechnen, wie viele m³ Gülle sie pro ha verteilt haben. Um dies zu üben, wurde in einer Klasse zuerst ein Beispiel für ein Feld von 200 m auf 258 m berechnet, auf das 156 m³ Gülle ausgetragen werden. Die Fläche des Feldes beträgt 5.16 ha. Also werden rund 30 m²/ha eingesetzt, was den üblichen Vorgaben entspricht. Die Lernenden hatten mit dieser Aufgabe keine grossen Schwierigkeiten. Als zweites folgte dann eine Aufgabe mit einem kleineren Feld: 48 m auf 68 m und 10 m³ Gülle. Die Fläche ist hier 0.32 ha und es ergeben sich wieder etwa 30 m³/ha. An dieser Stelle stutzten nun einige Lernende: Sie haben ja nur 10 m³ Gülle ausgetragen; wie kann es denn sein, dass es im Resultat 30 m³ sind, also viel mehr?

Die Verwirrung dieser Lernenden lässt sich lösen, wenn man sie fragt, was denn geschehen wäre, wenn sie mit ihrem Traktor genau gleich weitergefahren wären, bis sie eine ganze ha abgedeckt hätten. Nach einigen Hin-und-Her erkennen sie, dass 30 m³/ha in beiden Aufgaben im Sinn von „was wäre wenn“ verstanden werden muss: Wie viel hätte ich verbraucht, wenn ich auf diese Art genau eine ha bearbeitet hätte?

Dieselbe Vorstellung ist wichtig für alle Angaben dieser Art. Die errechneten 60 km/h nachdem man in einer halben Stunde 30 km zurückgelegt hat, bedeutet auch: Wie weit wäre ich gekommen, wenn ich auf die genau gleiche Art genau eine Stunde gefahren wäre? Etc.

Interessant ist übrigens, dass man bei diesen Quotienten-Grössen auch einmal „falsch“ rechnen darf (bezogen auf die Regeln des klassischen Bruchrechnens).  Nehmen wir an, Cristiano Ronaldo hat im Hinspiel 3/4 (drei von vier) Tore geschossen und im Rückspiel 2/3 (zwei von drei). Dann ist es völlig in Ordnung, die zwei „Zähler“ (3+2=5) und die zwei „Nenner“ (3+4=7) zu addieren um zum Schluss zu kommen, dass er insgesamt 5/7 (fünf von sieben) Tore geschossen hat.

2.3 Proportionen

Ab und zu treten Bruchstriche in „Formeln“ auf, die den Zusammenhang zwischen der Verhältnissen verschiedener Grössen beschreiben. Bekannte Beispiele dafür sind:

Brechungsgesetz: Wechselt ein Lichtstrahl von einem Medium (bspw. Luft) in ein anderes Medium (bspw. Wasser), dann ändert er seine Richtung.

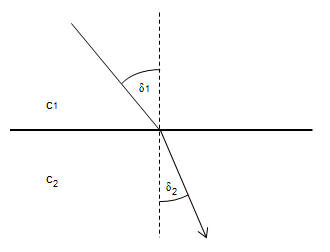
Wie stark das geschieht, hängt von der Geschwindigkeit des Lichts in den beiden Medien ab (kurz c₁ und c₂). Trifft das Licht im Winkel d₁ aus dem Medium 1 herkommend auf die Grenzfläche, dann wird es diese Fläche im Medium 2 im Winkel d₂ verlassen. Dabei gilt: Die beiden Winkel (bzw. deren Sinus) stehen zueinander im gleichen Verhältnis wie die beiden Lichtgeschwindigkeiten.

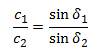
Mischrechnung: Braucht beispielsweise eine Milchtechnologin Milch mit einem Fettgehalt von 1.9%, dann wird sie diese typischerweise herstellen, indem sie zwei Milchsorten mit je einem höheren und einem tieferen Fettgehalt mischt (M₁ und M₂). Typische Ausgangssorten sind Vollmilch mit einem Fettgehalt von beispielsweise 3.8% sowie Magermilch mit einem Fettgehalt von 0.05%. Wieviel es von jeder Sorte braucht, hängt davon ab, wie stark der Fettgehalt der einzelnen Sorte vom erwünschten Fettgehalt abweicht (DF₁ und DF₂). Weicht eine Sorte nur wenig ab, dann gleicht die gewünschte Mischung stark dieser Sorte und man kann viel von dieser Sorte nehmen. Es gilt: Das Verhältnis der beiden Teilmengen M₁ und M₂ zueinander entspricht dem umgekehrten Verhältnis der Abweichungen im Fettgehalt DF₁ und DF₂. (Genau diesen Zusammenhang nutzt das sogenannte „Mischkreuz“).

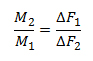
Ich denke, es ist überflüssig, an dieser Stelle nochmals zu betonen, dass auch hier die Vorstellung „Teil eines Ganzen“ nicht weiter hilft. Wichtiger ist zu sehen, dass hier ein System von vier Grössen dargestellt wird, die auf eine ganz bestimmte Art und Weise zusammenwirken. Fixiert man zwei dieser Grössen auf einen festen Wert und variiert man eine dritte, dann verändert sich als Folge davon die vierte Grösse auf eine ganze bestimmte Art und Weise.

Fixiert man beispielsweise beim Brechungsgesetzt das erste Medium (also c₁) und den Einfallswinkel (also d₁), dann kann man untersuchen, wie sich der Ausfallswinkel d₂ ändert, wenn man das zweite Medium (also c₂) verändert. Beispielsweise:

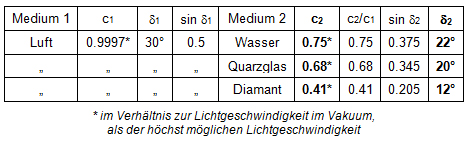
Nicht alle möglichen Kombinationen von fixen und variablen Werten entsprechen praktisch relevanten Situationen. So dürfte sich im praktischen Alltag der Milchtechnologen wohl kaum je die Frage stellen, wie sich der Fettgehalt der zweiten Menge ändern muss, wenn man das Verhältnis der beiden Mengen zueinander (M₁/M₂) fix hält und den Fettgehalt der ersten Menge ändert. Sich das zu überlegen, ist eine hübsche geistige Turnübung aber praktisch kaum relevant. Hingegen dürfte es wichtig sein, eine Vorstellung davon zu haben, wie sich das Verhältnis der beiden Mengen zueinander ändern muss, wenn der Fettgehalt der einen Menge fix ist und man den Fettgehalt der anderen Menge variiert (also beispielsweise Vollmilch mit 4.1% anstatt 3.8% Fettgehalt einsetzt).

Neben der Vorstellung, wie sich die Veränderung einer Grösse auf eine andere auswirkt, dürfte es auch wichtig sein, eine zumindest intuitive Begründung dafür zu haben, warum die Zusammenhänge so sind, wie sie in den jeweiligen Formeln zum Ausdruck kommen. Für die Mischrechnung habe ich oben versucht, eine solche Begründung zu geben: Je ähnlicher beispielsweise der Fettgehalt eine Sorte dem Fettgehalt der gewünschten Mischung ist, umso mehr nimmt man von dieser Sorte; je unähnlicher, umso weniger.

Auch beim Brechungsgesetz ist eine intuitive Begründung möglich. Man kann sich das Licht, das auf die Grenzfläche zwischen bei beiden Medien trifft, als Welle vorstellen (in der Skizze unten angedeutet als hintereinander herlaufende Wellenberge). Wie man sieht, trifft die eine Seite der Welle früher auf das zweite Medium, wird also früher gebremst, als die andere, die noch mit der alten Geschwindigkeit weiterläuft. Dadurch wird die Welle etwas gedreht.

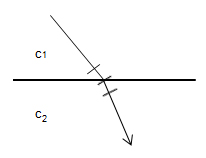
Das Brechungsgesetzt wird üblicherweise nicht mittels der beiden Geschwindigkeiten c₁ und c₂ sondern mittels der sogenannten Brechungsindizes der beiden Medien (kurz n₁ und n₂) formuliert: n₁/n₂ = sin(d₂)/sin(d₁). So dargestellt, ist der Zusammenhang aber intuitiv schwieriger nachvollziehbar, weil im „Brechungsindex“ im Gegensatz zu den unterschiedlichen Lichtgeschwindigkeiten nur das Resultat nicht aber die Ursache für die Winkeländerung sichtbar ist. Der Brechungsindex ist aber nichts anderes als der Kehrwert (vgl. 2.1 oben) der Lichtgeschwindigkeit (multipliziert mit der Lichtgeschwindigkeit im Vakuum), also n₁ = 1/c₁ x c_v. Man kann also jederzeit einfach zwischen Brechungsindex und Lichtgeschwindigkeit hin und her rechnen. Und ist man vertraut im Umgang mit Kehrwerten, weiss man auch, was dabei geschieht.

2.4 Innere Verhältnisse

Möchte man im Beispiel oben bei der Mischrechnung aus Magermilch (M₁; 0.05% Fettgehalt) und Vollmilch (M₂; 3.8% Fettgehalt) 1000 Liter Milch mit 2% Fettgehalt mischen, dann erhält man, wenn man in die Grundformel einsetzt:

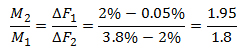
D.h. man muss Vollmilch zu Magermilch im Verhältnis von 1.95 zu 1.8 zusammenmischen (anschaulich: die gewünschten 2% liegen ein klein wenig näher bei den 3.8% als bei den 0.05%, daher braucht es ein klein wenig mehr Vollmilch als Magermilch).

Angaben dieser Art treten immer wieder auf, wie beispielsweise „Es haben sich doppelt so viele Mädchen wie Knaben angemeldet“ d.h. das Verhältnis von Knaben zu Mädchen ist 1:2. Bei dieser Art „Bruch“ ist tatsächlich ein Bezug zu einem „Ganzen“ gegeben, nur sind sowohl „2“ wie „1“ sich ergänzende Teile desselben „Ganzen“: Auf drei Kindern kommen jeweils 2 Mädchen und 1 Knabe bzw. 1/3 der Kinder sind Knaben, 2/3 sind Mädchen. Haben sich beispielsweise 90 Kinder angemeldet, so müssen das 30 Knaben und 60 Mädchen sein.

Angaben dieser Art bezeichnet man als innere Verhältnisse. Sie sind immer so zu verstehen, dass „Zähler“ und „Nenner“ dieses Bruches ein Teil des „Ganzen“ sind, welches „Zähler“ und „Nenner“ zusammen ausmachen. Im Beispiel oben bedeutet also m₂/m₁ = 1.95/1.8 dass das „Ganze“, worauf sich die Angaben 1.95 und 1.8 beziehen, 3.75 (=1.95+1.8) ist. Es wird 1.95/3.75= 52% Vollmilch und entsprechend 48% Magermilch benötigt. Auf 1000 Liter bezogen, sind das 520 Liter Vollmilch und 480 Liter Magermilch.

Wichtig ist hier also die Vorstellung, dass sich eine Angabe wie 1:2 zwar sehr wohl auf ein „Ganzes“ bezieht, dass dieses „Ganze“ aber nicht 1 ist (wie bei einem Bruch im engeren Sinn), sondern dass „Zähler“ und „Nenner“ zusammen dieses „Ganze“ ausmachen. „Knaben im Verhältnis 1:2“ heisst nicht „1/2, d.h. die Hälfte, sind Knaben“, sondern 1/3 sind Knaben.

2.5 Steigungen

Steigungen im Gelände werden je nach Berufsfeld auf verschiedene Arten angegeben. Üblich sind Angaben in Grad (30°, Steigungswinkeln), in Prozent (2%, Höhenunterschied in Prozent der Horizontaldistanz), als Verhältnis (3:2, Höhenunterschied : Horizontaldistanz) und als Bruch (1/200, Höhenunterschied/Horizontaldistanz).

Steigungsangaben sind Proportionen (ausser den Angaben in Grad):

Das eine der beiden Verhältnisse wird dabei quasi als Modell für das andere benutzt: „Das Verhältnis von Höhenunterschied zur Horizontaldistanz ist wie im Fall, wo man 200 Meter weit gehen muss, bis man 1 Meter gestiegen ist“. Die Darstellung des Verhältnisses, das als Modell dient, ist jeweils normiert. Bei Steigungsangaben wie 2% hat das Modell immer die Form „wenn man 1 Meter weit geht, steigt man soundso viele Zentimeter“. Bei Angaben wie 1/200, 1/220 etc. ist es immer „um 1 Meter zu steigen, muss man soundso viele Meter gehen“.

Indem man verschieden Fälle durch immer gleich normierte Modelle abbildet, werden die Fälle leichter vergleichbar. Sowohl zu einem Fall, bei dem es auf 4 km Horizontaldistanz um 4‘000 m nach oben geht, wie zu einem Fall, in dem es auf 2 m Horizontaldistanz um 2 m nach oben geht, passt das Modell 100%, d.h.: „Wenn man 1 Meter weit geht, steigt man um 100 cm“. Beide Fälle sind in dieser Hinsicht vergleichbar.

Steigungen teilen die Eigenart, dass reale Verhältnisse auf ein normiertes Modell bezogen werden mit den Quotienten-Grössen (vgl. 2.2 oben). Auch hier geht es um eine „was wäre wenn“ Überlegung. Wenn man anstatt nach 4 km Horizontaldistanz den Höhenunterschied zu messen, diesen bereits nach 1 Meter messen würde, wie gross wäre er dann? Für den Umgang mit Steigungen sind also einerseits dieselben Vorstellungen wichtig wie für die Quotienten-Grössen.

Andererseits teilen Steigungen mit den Proportionen die Eigenart, dass zwei Verhältnisse einander gleich gesetzt werden. Auch hier ist es beispielsweise so, dass man, wenn zwei der vier Grössen gegeben sind, ausprobieren kann, wie die vierte Grösse reagiert, wenn man die dritte verändert. Gegeben sind hier allerdings immer dieselben beiden Grössen, nämlich die beiden des Modells. Trotzdem sind für den Umgang mit Steigungen auch die Vorstellungen wichtig, die beim Umgang mit Proportionen eine Rolle spielen.

Folgendes Beispiel illustriert, wie man mit solchen Angaben nicht einfach „rechnen“ kann (Wake, 2014): Ein Ingenieur muss für eine Bahnstrecke die durchschnittliche Steigung berechnen. Die ganze Strecke zerfällt in zwei Teilstrecken mit folgenden Eigenschaften:

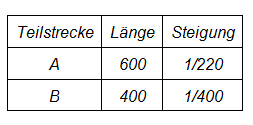
Man könnte nun versucht sein, die zwei „Brüche“ zu addieren und dann durch zwei zu teilen, um den Durchschnitt zu erhalten:

(1/220 + 1/400) : 2 =
(20/4400 + 11/4400) : 2 =
(31/4400) : 2 = 31/8800 ? 1/284

Schaut man sich die Situation aber genauer an, stellt man schnell fest, dass dies nicht ganz stimmt:

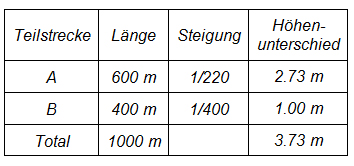
Dividiert man den gesamten Höhenunterschied durch die Gesamtlänge der zwei Teilstrecken, erhält man 3.73 / 1000 ? 1 / 268. D.h. die Gesamtstrecke ist im Durchschnitt etwas steiler, als der Wert, den man erhält, wenn man den Durchschnitt der Steigungen der beiden Teilstrecken nimmt. Das liegt daran, dass die zweite Teilstrecke etwas kürzer ist als erste, sie also etwas weniger Einfluss auf den gesamten Höhenunterschied hat und damit ihre geringere Steigung etwas weniger ins Gewicht fällt.

Das klassische Bruchrechnen funktioniert hier nicht, da sich die beiden „Brüche“ nicht auf dasselbe „Ganze“ beziehen. Die 1/220 beziehen sich auf einen 600 m langen Streckenabschnitt, die 1/400 auf einen 400 m langen. Dasselbe gilt übrigens auch, wenn man die Steigungen nicht als „Brüche“ sondern bspw. in Promille angibt, also 4.5‰ und 2.5‰, denn bei diesen Promilleangaben bezieht sich jeweils 1000‰ selbstverständlich genau so wenig auf dasselbe, wie die jeweiligen „Ganzen“ bei den Bruchangaben.

3 Die Vorstellungen kurz zusammengefasst

Kehrwerte: Wenn die eine Grösse sich verdoppelt, dann halbiert sich die andere. Wenn die eine Grösse sich um einen festen Betrag grösser wird, hängt die Wirkung davon ab, zu welchem Ausgangswert dieser Betrag addiert wird. (Beispiele: Widerstand = 1 / Leitwert; Brechungsindex = Lichtgeschwindigkeit im Vakuum / Lichtgeschwindigkeit)

Quotienten-Grössen: Wenn man mit der gleichen Geschwindigkeit weiterfahren würde bis eine Stunde vorbei ist, dann hätte man so und so viele Kilometer zurückgelegt. (Beispiele: km/h, kg/m³, m³/ha)

Proportionen: Die Formel steht für einen bestimmten, meist intuitiv nachvollziehbaren Zusammenhang zwischen vier Grössen. Typischerweise sind zwei davon bekannt. In diesem Fall kann man untersuchen, was mit der vierten Grösse geschieht, wenn man die dritte verändert. (Beispiele: c₁/c₂ = sin(d₁)/sin(d₂); M₁/M₂=DF₁/DF₂)

Innere Verhältnisse: Bei diesem „Bruch“ machen „Zähler“ und „Nenner“ zusammen das „Ganze“ aus. „Zähler“ und „Nenner“ stehen dann für je einen, sich ergänzenden Teil dieses „Ganzen“. (Beispiele: Knaben/Mädchen = 2/1; M₁/M₂ = 1.95/1.8)

Steigungsangaben: Eine Kombination der Vorstellungen zu Proportionen und zu Quotienten-Grössen (Beispiele: 1/2200; 2.5‰)

4 Weitere Bruchstriche

Neben den oben beschrieben Verwendungen von Bruchstrichen im beruflichen Kontext gibt es noch eine ganze Reihe weiterer, die an verschiedenen anderen Orten eine Rolle spielen. Ein paar Beispiele dazu:

Eine Zahl: 1/x stellvertretend für die Zahl, die man erhalten würde, wenn man 1 durch x teilen würde.

Wettquoten: 4/1 für das Verhältnis des Gewinns zum Einsatz, hier: Wer 1 Franken einsetzt, erhält 4 Franken, sofern er gewinnt.

Lottosysteme: 7/49 für „es müssen 7 von 49 Zahlen angekreuzt werden“ („7 aus 49“).

Sprachliche Abkürzungen: Manchmal treten Bruchstriche auch an Stellen auf, wo zwar so etwas wie eine Verhältnis angedeutet wird, aber eine eigentliche „mathematische“ Interpretation nicht möglich ist. Beispielsweise: 24/7 als Kurzformel für „sieben Tage die Woche rund um die Uhr“.

6 Erwähnte Literatur

• Malle, G. (2004). Grundvorstellungen zu Bruchzahlen. Mathematik lehren, 123, 4-8.
• Swanson, D., & Williams, J. (2014). Making abstract mathematics concrete in and out of school Educational Studies in Mathematics, 86(2), 193-209.
• Wake, G. (2014). Making sense of and with mathematics: the interface between academic mathematics and mathematics in practice. Educational Studies in Mathematics, 1-20. doi: 10.1007/s10649-014-9540-8