pdf Der folgende Text ist ein Versuch. Aus der Fachliteratur ist zwar bekannt, dass die hier angegangenen Probleme existieren. Was ich hier dazu geschrieben habe, ist aber am Schreibtisch entstanden und noch nicht erprobt. Es ist daher noch unklar, ob die hier gewählte Darstellung für Berufsschullehrpersonen verständlich und nützlich ist. Für Rückmeldungen bin ich dankbar!

Eine Aufgabe aus der vierten Klasse (Prediger 2010):

Lisa rechnet 24 x 7 so:
24 x 7 = 20 x 7 + 4 x 7 = 140 + 28 = 168.
i) Hat sie das richtig gemacht? Wie würdest Du das machen? 
ii) Berechne 54 x 6 so wie es Lisa gemacht hat.

Emily (10 Jahre alt) protestiert: „Lisa rechnet nicht richtig; 24 mal 7 ist nicht 20! Und was ist denn das nach der 20?“ Sie macht dann mit der Aufgabe nicht mehr weiter. Und dies, obwohl sie selbst normalerweise auch wie Lisa vorgeht und 24 x 7 in 20 x 7 und 4 x 7 zerlegt.

Emilys Problem ist offenbar nicht, dass sie nicht rechnen kann. Ihr Problem ist, dass sie nicht versteht, wie hier das Gleichheitszeichen eingesetzt wird. Das ist kein Wunder, denn es gibt mindestens sechs verschiedene Arten, das Gleichheitszeichen zu verwenden (Prediger 2010).

1 Operation und Relation

Emily ist sich an Aufgaben der Art

              24 : 6 - 3 =

gewohnt. Dort ist das Gleichheitszeichen eine Aufforderung, etwas zu tun: „Schreibe dahinter die Antwort!“ Diese Antwort ist immer eine Zahl, in diesem Fall 1. Entsprechend interpretiert sie auch in 24 x 7 = 20 das Gleichheitszeichen als Operation: Lisa hat 24 x 7 gerechnet und hinter dem Gleichheitszeichen 20 als Resultat notiert.

In der Aufgabe ist aber mit

              24 x 7 = 20 x 7 + 4 x 7

eine Relation gemeint: Auf beiden Seiten des Gleichheitszeichens steht (in einem gewissen Sinn) dasselbe (Prediger 2010). Diese Bedeutung des Gleichheitszeichens ist für Emily, wenn nicht gerade ganz neu, so doch zumindest unvertraut. Entsprechend verwirrt reagiert sie. Genau gleich geht es Lernenden, die beispielsweise zum ersten Mal die „Formel“ U = R x I sehen. In welchem Sinn kann R x I das Resultat von U sein? Überhaupt, wie kann U ein Resultat haben?

Die Lernenden haben typischerweise in ihrer Schullaufbahn zuerst das Gleichheitszeichen als Operations-Zeichen angetroffen und die meisten haben noch vergleichsweise wenig Erfahrungen mit dem Gleichheitszeichen als Relations-Zeichen. Daher ist zu erwarten, dass sich die Interpretation als Operation immer wieder in den Vordergrund drängt. Entsprechend wichtig ist es, im Unterricht bewusst und explizit auf diesen Unterschied hinzuweisen.

Etwas vorbeugen kann man, indem man das Gleichheitszeichen nie in „Kettenrechnungen“ der folgenden Art einsetzt:

              24 : 6 = 4 - 3 = 1 !!

Hier kann das Gleichheitszeichen nur als Operation verstanden werden („Ich rechne 24 : 6 und erhalte 4; dann rechne ich weiter 4 – 3 und erhalte 1“). Im Gegensatz dazu können in

              24 : 6 - 3 = 1

beide Bedeutungen ohne Widerspruch nebeneinander bestehen („Ich rechne 24 : 6 – 3 und erhalte 1“ und „24 : 6 – 3 und 1 sind gleich“).

2 Formale Gleichheit und kontextgebundene Gleichheit

Die Art der Relation, welche in

             24 x 7 = 20 x 7 + 4 x 7

oder auch in

              5 x 7 = 7 x 5

zum Ausdruck kommt, bezeichnet eine arithmetische Gleichheit und bedeutet im Wesentlichen: Man kann das so oder so rechnen; das Resultat ist dasselbe.

Aber auch für Lernende, welche mit dieser Unterscheidung zwischen Operation und Relation zurechtkommen, sind noch lange nicht alle Ursachen für Verwirrungen und Missverständnisse ausgeräumt (Prediger 2010). In den beiden folgenden Formeln steht das Gleichheitszeichen zwar in beiden Fällen für die Gleichheit der beiden Seiten. Es ist aber nicht dieselbe Art von Gleichheit:

              (a-b)(a+b)=a²-b²

              a²+b²=c²

Die erste Gleichheit gilt immer und unter allen Umständen. Die Formal drückt aus, dass die beiden Seiten der Gleichung formal gleich sind, dass die eine immer für die andere einstehen kann. Egal welche Zahlen man für a und b einsetzt, man wird auf beiden Seiten der Gleichung dasselbe Resultat erhalten. Gleichheit bedeutet hier also: Man kann das auf die eine wie die andere Art berechnen; es spielt keine Rolle, welche Variante man wählt – ganz ähnlich wie im konkreten Fall von 5 x 7 = 7 x 5.

Ganz im Gegensatz dazu die zweite der beiden Gleichungen. Hier gilt keinesfalls, dass man beliebige Zahlen für a, b und c einsetzen kann. Etwa 2²+3² ist nicht gleich 4². Die Gleichheit gilt nur in einem bestimmten Kontext, bei einer bestimmten Interpretation. Hier gilt sie, wenn man für a, b und c die Seitenlängen eines rechtwinkligen Dreiecks einsetzt, wo bei c die Länge der Seite gegenüber dem rechten Winkel (der Hypotenuse) sein muss. Nur wenn diese Bedingungen erfüllt sind, kann man diese kontextgebundene Gleichheit genauso nutzen, wie die formale Gleichheit oben: Egal welche Seite der Gleichung man berechnet, man kennt damit auch das Resultat, welches die Berechnung der anderen Seite ergeben würde.

Die Lernenden treffen im Zusammenhang von für ihren jeweiligen Beruf wichtigen Formeln (wie etwa U = R x I) vor allem kontextgebundene Gleichheit an. Es ist auch wichtig, dass sie diese Gleichungen so verstehen, dass ihnen bewusst ist, dass diese eine mathematische Beschreibung eines realen Zusammenhangs sind. Das dürfte den Lernenden nicht so ohne weiteres klar sein, denn in ihrem bisherigen Mathematikunterricht haben sie sich mehrheitlich mit formaler Gleichheit beschäftigt, haben erkundet, welche Zusammenhänge zwischen Zahlen bestehen, unabhängig davon wofür diese Zahlen stehen (für ein Beispiel s. Abschnitt 7 unten). Entsprechend ist es wichtig, explizit zum Thema zu machen, dass eine solche kontextgebundene Gleichheit ein Modell für einen real gegeben Zusammenhang ist, den zuerst irgendjemand einmal entdecken musste.

3 Bedingungen für eine Unbekannte

Die oben beschriebene kontextgebundene Gleichheit könnte man als allgemeine kontextgebundene Gleichheit bezeichnen. U = R x I steht dafür, dass in jedem Stromkreis dieser Zusammenhang zwischen Spannung (U), Widerstand (R) und Stromstärke (I) besteht. Es gibt unendlich viele Tripel <U,R,I>, unter denen man wählen kann, um die Gleichung zu erfüllen. Sind hingegen beispielsweise U und R bekannt, dann kann man I nicht mehr beliebig wählen. Beispielsweise ist mit

              220 Volt = 100 Ohm x I

für I nur noch ein Wert möglich, nämlich 2.2 Ampere. Man könnte in diesem Fall von einer spezifischen kontextgebundenen Gleichheit sprechen. Der Kontext ist so klar gegeben, dass es für eine bestimmte Grösse, an der man interessiert ist, die man aber nicht direkt kennt, nur noch eine (oder manchmal einige wenige) Möglichkeiten gibt. In diesem Fall beschreibt die Gleichung nicht einen allgemeinen Zusammenhang (Stromkreise im Allgemeinen) sondern einen spezifischen (einen ganz bestimmten Stromkreis).

Haben die Lernenden die allgemeine kontextgebundene Gleichheit verstanden, die in Formeln wie U = R x I zum Ausdruck kommt, dann sollten sie mit dieser spezifischen Varianten davon keine Mühe haben.

Ausserhalb der Berufsbildung können Gleichungen dieser Art auch ohne Bezug auf einen bestimmten Kontext vorkommen. Die Gleichung

              x² = 6 - x

definiert Rahmenbedingungen, welche die Unbekannte x erfüllen muss (Prediger 2010), auch ohne dass man x eine inhaltliche Interpretation gibt. In diesem Fall gibt es zwei mögliche Wert für x, welche diese Gleichung erfüllen: 2 und -3.

4 Definitionen

Und nicht zuletzt tritt das Gleichheitszeichen auch in Definitionen auf (Prediger 2010). Die Steigung einer Strasse beispielsweise ist definiert als das Verhältnis des Höhenunterschieds zur Horizontaldistanz; oder in Form einer Gleichung

               m = Dy/Dx

Diese Gleichung bezieht sich zwar auf einen bestimmten Kontext. Die einzelnen Grössen haben eine bestimmte Interpretation und die Gleichheit gilt nur in diesem Zusammenhang, so wie das auch bei der kontextgebundenen Gleichheit (s.o.) der Fall ist. Nur wird hier nicht ein Zusammenhang zwischen drei unabhängig messbaren Grössen mathematisch beschrieben, sondern die dritte Grösse, die Steigung, wird mittels der beiden anderen definiert. Die Gleichheit ist in diesem Fall also willkürlich. Man hätte auch etwas anderes festlegen können (beispielsweise m = Dy³/Dx²), aber man hat sich nun einmal für diese Variante entschieden.

Es geht hier also nicht um eine Gesetzmässigkeit, sondern um eine willkürlich Festlegung, welche aus bestimmten praktischen Erwägungen heraus getroffen wurde. Bei Lernenden, für die „Mathematik“ aus unumstösslichen Wahrheiten aufgebaut ist („2+2 ist nun einmal 4“), kann dieses Element der Willkürlichkeit verwirrend sein und muss thematisiert werden. Ein guter Anknüpfungspunkt ist die Frage, warum wohl genau diese Definition gewählt wurde. Ein Gefühl dafür können die Lernenden gewinnen, wenn sie Gelegenheit erhalten, spielerisch alternativen Definitionen zu erkunden.

Solche willkürlichen Definitionen sind häufiger, als man denkt. Beispielsweise sind die ganzen trigonometrischen Funktionen wie Sinus (=Gegenkathete/Hypotenuse), Cosinus (=Ankathete/Hypotenuse) und Tangens (=Gegenkathete/Ankathete) Grössen, die sich zwar als nützlich erwiesen haben, die man aber auch anders hätte definieren können.

5 Die verschiedenen Bedeutungen kurz zusammengefasst

Alles in allem müssen also mindestens die folgenden Bedeutungen unterschieden werden (Prediger 2010). Gelingt das den Lernenden nicht, sind Verwirrungen und Missverständnisse unvermeidlich.

1. Operation
   • „Hier kommt die Antwort“: 24 : 6 – 3 = 1
2. Relation
   • „Man kann das so oder so rechnen“
     (symmetrische arithmetische Gleichheit): 5 x 7 = 7 x 5
   • „Für beliebige Zahlen erhält man auf beiden Seiten dasselbe Resultat“
     (formale Gleichheit): (a-b)(a+b)=a²-b²
   • „Zwischen bestimmten Grössen/Messwerten gilt“
     (allgemeine kontextgebundene Gleichheit): Rechtwinkliges Dreieck, c Hypotenuse, a²+b²=c²
   • „In diesem konkreten Fall gilt zwischen bestimmten Grössen/Messwerten“
     (spezifische kontextgebundene Gleichheit): Ein bestimmter Stromkreis, U Spannung, R Widerstand, I Stromstärke, 220 Volt = 100 Ohm x I
   • „Die gesuchte Grösse muss folgende Bedingungen erfüllen“
     (Bedingungen für eine Unbekannte): gesucht x; es gilt x²=6-x
3. Definition
   • „Eine bestimmte Grösse ist wie folgt definiert“:
     m = Dy/Dx (m: Steigung; Dy: Höhendifferenz; Dx: horizontale Distanz)

6 Anhang: Wechselnde Bedeutungen – Ein Beispiel

Prediger untersucht in ihrem Artikel (2010), wie im Verlauf der Bearbeitung einer Aufgabe das Gleichheitszeichen ständig die Bedeutung wechselt. Die Aufgabe ist eine klassische Aufgabe, wie sie im Mathematikunterricht am Gymnasium kurz vor der Matura vorkommt.

Zeige, dass von allen Rechtecken mit demselben Umfang 
das Quadrat (also das Rechteck mit vier gleich langen 
Seiten) die grösste Fläche hat.

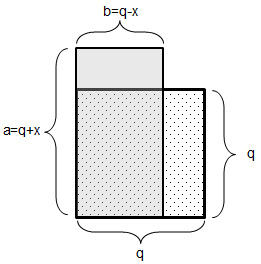
(1)       In einem Quadrat mit der Seitenlänge q ist U = 4q (U: Umfang)	allgemeine kontextgebundene Gleichheit
(2)       In jedem Rechteck mit diesem Umfang gilt für die beiden Seiten a und b: a=q+x und b=q-x	allgemeine kontextgebundene Gleichheit
(3)       Die Fläche F dieser Rechtecke ist jeweils F=(q+x)(q-x)	allgemeine kontextgebundene Gleichheit
(4)       F = q2-x2	formale Gleichheit
(5)       Sei F(x) die Funktion F(x)= q2-x2	Definition
(6)       Erste Ableitung F‘(x) = -2x	Operation
(7)       Zweite Ableitung F‘‘(x) = -2	Operation
(8)       Für jedes lokale Maximum ist F‘(xe)=0 und F‘‘(xe)<0	allgemeine kontextgebundene Gleichheit
(9)       Sei F‘(xe) = -2xe = 0	Bedingungen für eine Unbekannte
(10)    mögliches Maximum xe = 0	Operation
(11)    F‘‘(0) = -2	Operation
(12)    Also hat F(x) tatsächlich bei xe=0 ein Maximum, d.h. das Quadrat hat die grösste Fläche von allen Rechtecken mit dem gleichen Umfang	allgemeine kontextgebundene Gleichheit

 7 Anhang: Untersuchen formaler Gleichheit – ein Beispiel

Die folgende Aufgabe stammt aus dem Buch von Hirt & Wälti (2008, S. 86ff) und ist für die dritte bis sechste Klasse gedacht:

Startzahl: 1
Pluszahl: 2
Zielzahl: 25
              1 + 3 + 5 + 7 + 9 = 25

i) Wähle die Startzahl und die Pluszahl so,
   dass die Zielzahl möglichst nahe an „50“ 
   herankommt.
ii) Finde möglichst viele Beispiele mit der 
    Zielzahl „50“. Vergleiche die Beispiele 
    und beschreibe deine Feststellungen.

Beim Bearbeiten dieser Aufgabe kann man beispielsweise folgendes herausfinden: Ist a die Startzahl und b die Pluszahl, dann lässt sich die Berechnung der Zielzahl beschreiben als

a + (a+b) + (a+b+b) + (a+b+b+b) + (a+b+b+b+b) = Zielzahl

Das ist formal gleich mit

              5a + 10b = Zielzahl
              5 (a+2b) = Zielzahl

Und daraus kann man beispielsweise ablesen, dass die Zielzahl immer durch 5 teilbar ist, gleichgültig wie man a und b wählt.

8 Literatur

• Hirt, U., & Wälti, B. (2008). Lernumgebungen im Mathematikunterricht. Natürliche Differenzierung für Rechenschwache bis Hochbegabte. Seelze-Velber: Kallmeyer.
• Prediger, S. (2010). How to Develop Mathematics for Teaching and for Understanding. The Case of Meanings of the Equal Sign Journal for Mathematics Teacher Education, 13(1), 73-93.