pdf Der didaktische Ablauf in acht Schritten kommt ohne eigentliches Lehrmittel aus: Erfahrungen schildern lassen, die Lösungen in Gruppen diskutieren, eigene Beispiele erfinden und bearbeiten, Spickzettel erarbeiten, Anwendung im Betrieb diskutieren etc. sind alles Aktivitäten, die vielleicht einer kleinen Anleitung, aber sicher nicht eines „Lehrmittels“ bedürfen.

Um aber Lehrende und Lernende über die acht Schritte hinweg eine Art roten Faden in die Hand zu geben, kann man pro Situation eine sogenannte „Lernumgebung“ kreieren. Die hier vorgeschlagene Form der Lernumgebung besteht aus einen A3 Blatt, auf dem verschiedenen Informationen und Anregungen zur jeweiligen Situation zusammengestellt sind. Als Beispiel die Lernumgebung „Rezeptangaben umrechnen“.

Anklicken öffnet eine A3 grosse pdf Datei

Vielleicht können Sie den folgenden Ausführungen besser folgen, wenn Sie sich die grosse Version der Lernumgebung herunterladen und ausdrucken.

1. Aufbau der Lernumgebungen

Nützliche Elemente einer Lernumgebung sind:

1. Ein Titel und eine kurze Beschreibung der Situation
2. Einige einleitende Fragen zur Situation
3. Eine einheitliche Seitenaufteilung
4. Eine ausführliche Darstellung der Werkzeuge
5. Verschiedene Zusatzelemente wie Tipps, wichtige Daten, typische Beispiele
6. Einige Fragen zur notwendigen Genauigkeit der Berechnungen
7. Ein konsistenter Bearbeitungsweg

a) Titel und kurze Beschreibung der Situation

Rezeptangaben umrechnen

Rezepte – darf es etwas mehr sein?

Ein Rezept gilt immer für eine bestimmte Anzahl Personen. 
Meist muss man aber für mehr Personen kochen. Dann gilt 
es, die Angaben aus dem Rezept umzurechnen, um die 
benötigten Mengen der Zutaten zu kennen.

Hier wird die der Lernumgebung zugrunde liegende Situation kurz eingeführt. Einerseits sollte dabei für die Lernenden klar werden, wo diese Situation auftritt und welche Bedeutung sie hat. Andererseits wird die Situation so dargestellt, dass die „mathematische“ Anforderung sichtbar wird.

Position dem Blatt: Der Titel oben links und die kurze Beschreibung der Situation darunter.

b) Fragen zur Situation

Zum Ãœberlegen

Warum gilt ein Rezept immer nur für eine bestimmte Anzahl 
Personen?
Welche Anzahl Personen ist in Rezepten üblich?
Oben steht: «Meist muss man aber für mehr Perso­nen 
kochen». Stimmt das? Kommen Ihnen auch Situationen in 
den Sinn, in denen für weniger Perso­nen zu kochen ist, 
als im Rezept steht?

Die Fragen sollen die Lernenden anregen, sich in die Problematik der Situation hineinzudenken. Darunter können auch „dumme“ Fragen sein, Fragen, die auf den ersten Blick verwirren, die aber beim genaueren Nachdenken die „mathematische“ Struktur der Situation erhellen.

Position: Ein Kasten in der Nähe des Titels. (Im Beispiel „Rezeptangaben umrechnen“ ist der Kasten aus Gründen des Layouts etwas weit weg vom Titel gelandet.)

c) Seitenaufteilung

Das Arbeiten mit den Lernumgebungen wird erleichtert, wenn die beiden Halbseiten links und rechts immer etwa dieselbe Funktion übernehmen. Die linke Seite dient eher vorbereitenden Überlegungen wie Fragen zur Situation oder der Darstellung von Hilfswerkzeugen. Die rechte Seite ist dann dem Hauptwerkzeug gewidmet.

d) Werkzeuge

(vgl. Tabellen statt Formel, Mathematische Instrumente modernisieren und Rituale, Werkzeuge und Modelle)

Hilfswerkzeuge

Verdoppeln, Halbieren

Manchmal geht es im Kopf schneller als mit 
dem Taschenrechner.

Gibt es andere praktische Sprünge nach oben und unten?

Abschätzen

Benutzt man den Rechner, gibt es manchmal Tippfehler. 
Kurz abschätzen, ob das Resultat stimmen kann, lohnt 
sich deshalb.

Die Übungen können Sie leicht selbst fortsetzen, indem 
Sie weitere Beispiele erfinden, etwa indem Sie die 
Zahlen oben anders kombinieren. Z.B.

Hauptwerkzeug

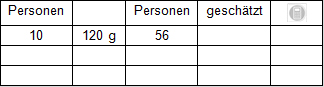
Bauen Sie die Tabelle so aus, dass Sie jederzeit bequem 
die Menge für z.B. 56 Personen, 32 Personen, 311 Personen 
etc. herauslesen können.

Erstellen Sie ähnliche Tabellen für beliebige andere 
Gerichte, z.B. für die Thurgauer Apfeltorte.

Sind die Personenzahlen 5, 10, 50 und 100 nützlich? 
Oder gibt es andere Werte, die nützlicher sind?

Wie steht es bei der Thurgauer Apfeltorte? Was machen
Sie, wenn Sie Torten für 12, 30 oder 42 Personen backen 
müssen?

Das Hauptwerkzeug ist das Werkzeug, das man den Lernenden als eigentliches Werkzeug zur Bewältigung der Situation vorschlägt (Schritt 5 der Acht Schritte).

Hilfswerkzeuge können etwa Umrechnungen von einer Einheit in eine andere, Grössen, die man auswendig kennen muss, oder auch Schätzübungen sein. Oft kann man davon ausgehen, dass den Lernenden diese Hilfswerkzeuge bekannt sind. Trotzdem kann sinnvoll sein, sie zu (re)aktivieren.

Die jeweiligen Werkzeuge werden in ihrem Gebrauch ganz kurz eingeführt. Dann folgen einige wenige Einsatzbeispiele. Das erste Beispiel ist als Modell vollständig gelöst. Bei den folgenden Beispielen müssen immer mehr Grössen durch die Lernenden erschlossen bzw. berechnet werden. Abschliessend folgt immer die Aufgabe, weitere Beispiele mit Angaben aus dem eigenen Betrieb zu bearbeiten.

Position: Entsprechend der vorgeschlagenen Seitenaufteilung gehören die Hilfswerkzeuge auf die linke Seite und das Hauptwerkzeug auf die rechte Seite. Im Beispiel „Rezeptangaben umrechnen“ sind dies als Hilfswerkzeuge „Verdoppeln, Halbieren“ und „Abschätzen“ sowie als Hauptwerkzeug eine Tabelle mit allen Zutaten und unterschiedlichen Personenzahlen.

 e) Tipps, Daten, Beispiele

Beispiel aus Kochbuch

Thurgauer Apfeltorte 

Zutaten für 18 Personen: 
4 feste Äpfel, 2 Eier, 200 g Zucker, 1 Päckli 
Vanillezucker, 100 g Butter flüssig, 100 g Mehl, 
½ Päckli Backpulver, Zitronensaft

Zubereitung: Äpfel grob raffeln und mit Zitronensaft 
beträufeln. Eier und Zucker schaumig rühren und 
Vanillezucker beigeben. Butter, Mehl und Backpulver 
beimischen, wenn nötig etwas Milch beigeben. 

Teigmasse in eine ausgebutterte Springform geben 
und die geraffelten Äpfel darauf verteilen. Bei 
180 °C auf der untersten Rille etwa 45 Minuten backen. 
Noch heiss mit Puderzucker bestreuen, lauwarm servieren.

 

Beispiel aus Rezeptbuch

Crème Caramel 

Zutaten für 5 Personen: 
10 g Butter
100 g Zucker
1/4 l Milch
1/4 l Vollrahm
100 g Zucker
2 Eier
3 Eigelb
1/2 Stange Vanille

Zubereitung: Für die Caramelsauce, die Butter in eine 
Pfanne geben und erhitzen. 100 Gramm Zucker darin unter 
ständigem Rühren schmelzen lassen, bis die Masse 
zartbraun ist.

In kleine feuerfeste Förmchen giessen. Eier, Eigelb 
und 100 Gramm Zucker schaumig schlagen. Nach und 
nach kochend heisse Milch mit dem Schneebesen 
einschlagen. Vanilleschote aufschlitzen, das Mark 
heraus­kratzen und in die Crème geben.

Crème über die Caramelsauce in die Förm­chen giessen. 
Im Wasserbad in den Backofen bei 160 °C (mittlere 
Schiene) schieben und pochieren bis die Crème gestockt 
ist (ca. 30 – 40 Minuten).

Je nach Bedarf sind über die Lernumgebungen Kästchen verteilt, die nützliche Tipps, wichtige Daten oder anschauliche Beispiele enthalten.

Position: Diese Kästchen können frei zur graphischen Gestaltung und Auflockerung der Seite verteilt werden.

f) Fragen zur Genauigkeit

Beispiel im Internet 

Bei Rezepten, die im Internet publiziert werden, 
kann man oft die Anzahl Personen eingeben und der 
Computer berechnet dann die notwendigen Mengen. 
Wenn man beim Rezept "Rüebli gedämpft nach 
Militärkochbuch" für die Personen Zahl 77 eingibt, 
erhält man folgende Werte:

Gedämpfte Rüebli nach Militärkochbuch 
Zutat:          Menge:
Butter          770 g
Rüebli          10.010000000000002 kg
Wasser          38,5 dl
Bouillonwürfel  7,7 Stück

Die Fragen im Kasten „Genauigkeit“ sollen zum Nachdenken darüber anregen, unter welchen Umständen die errechneten Werte wie „genau“ bzw. wie „ernst“ genommen werden müssen und wo man sonstiges Fachwissen bzw. den gesunden Menschenverstand nicht ausser Acht lassen darf.

Position: Da Fragen und Diskussionen zur Genauigkeit am besten erst dann geführt werden, wenn die Lernenden mit dem Hauptwerkzeug vertraut sind, gehören sie an den Schluss, d.h. nach rechts unten auf dem Blatt. Im Beispiel „Rezeptangaben umrechnen“ gibt es neben dem „Beispiel aus dem Internet“ noch die Frage zur „Prise Muskatnuss“, die ebenfalls dazu anregen soll, wann es überhaupt möglich und sinnvoll ist, zu rechnen.

Zum Ãœberlegen
In einem Rezept für 12 Personen benötigt man 1 Prise 
Muskatnuss. Wie viel Muskatnuss braucht es bei 100 
Personen?

g) Bearbeitungsweg

Durch den hier beschreiben Aufbau ergibt sich innerhalb des Blattes eine Bewegung von oben links nach unten rechts. Oben links: Eintauchen in die Situation ausgehend von alltäglichen Vorstellungen. Ãœber das Blatt hinweg: „Leben“ mit den Rechenverfahren im Wechselspiel zwischen vorgegeben Beispielen und der Situation in den Betrieben. Unten rechts: Ausstieg aus dem „blinden Rechnen“, kritische Auseinandersetzung mit den Möglichkeiten und Grenzen des Gelernten.

2. Didaktischer Begleittext

Für Lehrende, die bei der Entwicklung der Lernumgebungen nicht dabei waren, ist nicht immer alles auf diesen Blättern selbsterklärend und nicht immer alle Ideen, die dahinter standen, sind sofort ersichtlich. Es ist deshalb zweckmässig, zu jeder Lernumgebung einen kurzen didaktischen Begleittext zu verfassen. Hier als Beispiel und Anregung der Text zu „Rezeptangaben umrechnen“.

---

Rezeptangaben umrechnen

---

1 Überlegungsaufgaben zum Verständnis der Situation

Die Situation ist vermutlich den meisten Lernenden vertraut. Die Überlegungsaufgaben (links) zielen daher eher darauf ab, der vertrauten Situation ein paar neue Perspektiven abzugewinnen. Eingesetzt werden können sie zu einem beliebigen Zeitpunkt während der Arbeit mit der Lernumgebung.

2 Zentrale Angaben, Grössen, etc.

Die Lernumgebung enthält keine Elemente zu diesem Punkt. Es wird davon ausgegangen, dass die Lernenden mit den üblichen Masseinheiten wie Liter, Deziliter, Milliliter, Kilogramm, Gramm, etc. umgehen können.

3 Angepasste mathematische Werkzeuge

Das traditionell in der Schule für das Umrechnen von Rezepten behandelte mathematische Werkzeug ist der Dreisatz. Die Forschung zeigt nun aber, dass erfahrene Personen in der Praxis kaum je Dreisatzrechnungen einsetzen. Ihr bevorzugtes Instrument ist viel mehr die Operation mit zwei parallelen Skalen. Nehmen wir an, in einem Rezept für 10 Personen werden 800 Gramm Zucker verlangt. Es soll für 25 Personen gekocht werden.

Personen	Zucker (g)
5	400
10	800
20	1’600
25	2’000

Ausgangspunkt ist das Zahlenpaar 10/800. Eine Verdopplung führt zu 20/1’600. Es fehlen noch 5 Personen, was die Hälfte von 10/800 ist (5/400), so dass sich als Resultat das Paar 25/2’000 ergibt.

Gegenüber dem Dreisatz hat dieses Verfahren unter anderem den Vorteil, dass es viel weniger anfällig auf grobe Fehler ist. Es führt beispielsweise kaum je zu Kommafehlern. Das Verfahren kann auch sehr gut eingesetzt werden, um die Korrektheit eines mit mechanischen Hilfsmitteln (Taschenrechner, Kalkulationssoftware) erreichten Resultates abzuschätzen.

In der Lernumgebung wird deshalb das Erstellen von Wertetabellen als Instrument ins Zentrum gestellt (rechts oben). Unterstützend finden sich Schätzübungen und einfache Kopfrechnungsübungen im Bereich Verdoppeln und Halbieren.

4 Ãœbungsaufgaben zum Einsatz der Instrumente

Aufgaben sind sowohl zum Abschätzen (links unten) wie zum tabellarischen Zusammenstellen (rechts oben) skizziert. Die Lernenden können und sollen sich selbst oder gegenseitig beliebige solche Aufgaben stellen und diese bearbeiten, bis sie sich sicher fühlen. Dabei sollen sie sowohl den Taschenrechner/Computer wie ihren „Kopf“ einsetzen und jeweils die erhaltenen Werte kreuzweise überprüfen. Für die tabellarischen Zusammenstellungen können sowohl Papier und Bleistift wie auch Tabellenkalkulationsprogramme zum Einsatz gelangen.

5 Überlegungsaufgaben zu den Stärken und Schwächen der Instrumente

Jedes rechnerische Verfahren ist mit dem Problem behaftet, dass es eine Genauigkeit vorspiegelt, welche unter Umständen nicht gerechtfertigt ist. Dies gilt es vor allem bei der Frage, wie das Gelernte im Betrieb eingesetzt werden kann, zu berücksichtigen.

• Welche Genauigkeit ist sinnvoll?
• Braucht es Stellen hinter dem Komma?
• Wenn ja, wo?
• Gramm? Kilogramm? Liter? Zentiliter?
• Wie geht man mit Grössen wie halben Eiern, ¼ Prisen, 8 ½ Kuchen und Ähnlichem um?
• Wie versuchen professionelle Rezeptsammlungen, wie sie z.B. auch in elektronischer Form vorliegen, mit diesen Fragen umzugehen?

Die verschiedenen Überlegungsfragen im rechten Teil können solche Überlegungen unterstützen. Sinnvoll ist es, mit den Lernenden möglichst viele solcher Probleme zu besprechen, die sich beim praktischen Einsatz des Rechnens ergeben.

---

3 Etwas Hintergrund zu einzelnen Punkten

3.1 Die Verbindung zu den „Acht Schritten“

Schritt 2 „Erfahrungen schildern lassen“: Damit die Lernenden wissen, zu welcher Situation sie ihre Erfahrungen schildern sollen, muss man ihnen diese kurz beschreiben. Der Titel und die kleine Beschreibung darunter übernehmen diese Aufgabe in der Lernumgebung.

Schritt 3 „Mittelschwere Aufgabe stellen“: Die Beispiele – beim „Rezeptangaben umrechnen“ die beiden Rezepte – können die Funktion einer solchen Einstiegsaufgabe übernehmen.

Schritt 4 „Die Lösungen gemeinsam kritisch besprechen“: Die Fragen zur Situation – bei „Rezeptangaben umrechnen“ etwa „Warum gilt ein Rezept immer für eine bestimmte Anzahl Personen?“ – können helfen zu überlegen, ob ein bestimmtes Vorgehen wirklich den wichtigsten Anforderungen der Situation gerecht werden.

Schritt 5 „Werkzeuge einführen“: Die auf der Lernumgebung dargestellten Hilfs- und Hauptwerkzeuge führen eine Variante ein, wie man die rechnerischen Anforderungen der jeweiligen Situation kompetent bewältigen kann.

Schritt 6 „Eigene Beispiele erfinden lassen“: Die offenen Aufgaben wie „Erstellen Sie ähnliche Tabellen für beliebige andere Gerichte“ entsprechen direkt diesem Schritt.

Schritt 7 „Spickzettel erarbeiten“: Diesen Schritt unterstützen Aufgaben wie: „Stellen Sie eine nützliche Tabelle zusammen“.

Schritt 8 „Anwendung im Betrieb diskutieren“: Fragen/Hinweise zur sinnvollen Genauigkeit beim Rechnen sowie Überlegungsfragen wie die Frage zur Prise Muskatnuss enthalten Hinweise darauf, was bei der Anwendung im Betrieb zu bedenken ist.

3.2 Lernumgebungen in der modernen Mathematikdidaktik

Der Begriff der „Lernumgebung“ wurde durch das Projekt Mathe-2000 in die Mathematikdidaktik eingeführt. Wittmann forderte in diesem Zusammenhang (Wittmann, 1998; S. 337): „… Lernumgebungen müssen folgenden Kriterien genügen:

1. Sie müssen zentrale Ziele, Inhalte und Prinzipien des Mathematikunterrichts repräsentieren.
2. Sie müssen reiche Möglichkeiten für mathematische Aktivitäten von Schüler/-innen bieten.
3. Sie müssen flexibel sein und leicht an die speziellen Gegebenheiten einer bestimmten Klasse angepasst werden können.
4. Sie müssen mathematische, psychologische und pädagogische Aspekte des Lehrens und Lernens in einer ganzheitlichen Weise integrieren und daher ein weites Potential für empirische Forschungen bieten.“

In der Schweiz wurde die Idee der Lernumgebungen durch das Projekt „Lernumgebungen für Rechenschwache bis Hochbegabte“ aufgenommen. In diesem Zusammenhang wurde vor allem die Möglichkeit betont, mit Hilfe von Lernumgebungen schwächeren und stärkeren Lernenden gleichzeitig gerecht zu werden: „Lernumgebungen sind Aufgaben, die eine niedere Eingangsschwelle für langsamer lernende Kinder anbieten, die auch für Kinder mit Lernschwächen zugänglich sein sollen. Zugleich enthalten die gleichen Aufgaben dank ihrer Reichhaltigkeit aber auch Forderungen für schnell lernende und für mathematisch hochbegabte Kinder bereit.“ und „Die Kinder bestimmen individuell das Aktivitätsniveau, die Lösungswege und Darstellungsweisen und tauschen diese untereinander aus.“

Aus diesem Projekt sind zwei Sammlungen von Lernumgebungen entstanden (Hengartner, Hirt, Wälti, & Lupsingen, 2006; Hirt & Wälti, 2008). Bei den meisten dieser Lernumgebungen geht es zwar darum, dass die Lernenden mathematische Zusammenhänge (beispielsweise zum Bruchrechnen) verstehen und weniger darum, dass sie mathematische Werkzeuge auf reale Situationen anwenden. Sie enthalten aber interessante Beispiele dafür, wie man Lernumgebungen konstruieren kann, so dass sie „für alle – auch für die schwächeren – zugänglich [sind] und … ‚Rampen‘ für ein Bearbeiten auf höheren Niveaus“ enthalten. Im Rahmen der hier vorgeschlagenen Lernumgebungen kann man solche Differenzierungen erreichen, indem man in spezielle Kästchen auf dem Blatt verteilt weiterführende Fragen einfügt, die nicht von allen Lernenden bearbeitet werden müssen.

Lernumgebungen, die auch einen direkten Anwendungsbezug enthalten, findet man dann im mathbu.ch, einem Lehrmittel für die 7. bis 9. Klasse. Beispielsweise gibt es im Buch für die 9. Klasse eine Lernumgebung zur Frage „Wie genau ist genau?“ (s. 32/33). Sie wird eingeleitet durch die (Situations-)Beschreibung: „Die Rechnung 12· 15 hat nur ein einziges richtiges Ergebnis. Es ist genau 180 und kein bisschen mehr oder weniger. Genauigkeit ist ein wesentlicher Bestandteil der Mathematik. Beim Rechnen mit gemessenen Werten muss man sich immer überlegen, wie viele Ziffern im Ergebnis sinnvoll sind. Das Abschreiben aller Ziffern vom Taschenrechner ist meistens unsinnig.“

Als Einstiegsaufgabe folgt dann: „An den Olympischen Spielen 1972 in München wurden die Zeiten bei den Schwimmwettbewerben auf 1/1000 Sekunde genau gemessen. Die beiden Spitzenschwimmer erreichten im Schwimm-Final (400 m Lagen im 50-m-Becken) folgende Zeiten: Gold: Gunnar Larson 4: 31.981; Silber: Alexander Mc Kee 4: 31.983

• Wie viele Millimeter Vorsprung hatte Gunnar Larson auf Alexander Mc Kee?
• Eine Nachmessung der beiden Schwimmbahnen hat ergeben, dass die 50-m-Bahn von Alexander Mc Kee einen Millimeter länger war als die Bahn von Gunnar Larson. War die Rangliste gerecht? Begründe.
• Wie genau müsste das 50-m-Becken gebaut sein?
• Begründe, warum nach den Olympischen Spielen in München die Zeiten in den Schwimmwettbewerben wieder auf eine Hundertstelsekunde genau gemessen werden.“

Die hier vorgeschlagenen Lernumgebungen lehnen sich vom Layout her an die Lernumgebungen des mathbu.ch an. Dort wie hier ist alles, was zu einer Lernumgebung gehört, auf einer Doppelseite A4 (bzw. einer A3 Seite) dargestellt. Die Idee ist, dadurch den Lernenden, welche solche Lernumgebungen schon aus dem Unterricht der Sekundarstufe I (und der Primarschule; dort Zahlenbuch) kennen, sich leicht auch im Fachrechnen in der Berufsfachschule zurechtfinden.

4 Zitierte Literatur

• Hengartner, E., Hirt, U., Wälti, B., & Lupsingen, P. (2006). Lernumgebungen für Rechenschwache bis Hochbegabte. Natürliche Differenzierung im Mathematikunterricht. Zug: Klett und Balmer.
• Hirt, U., & Wälti, B. (2008). Lernumgebungen im Mathematikunterricht. Natürliche Differenzierung für Rechenschwache bis Hochbegabte. Seelze-Velber: Kallmeyer.
• Wittmann, E. C. (1998 ). Design und Erforschung von Lernumgebungen als Kern der Mathematikdidaktik. Beitrage zur Lehrerbildung, 16(3), 329-342.