pdf     Anna Sfard unterscheidet in einem Grundlagenwerk zur Mathematikdidaktik drei Formen „mathematischer Kommunikation“: Rituale, Taten (deeds) und Explorationen (Sfard, 2008, S. 222 ff).

Mit Kommunikation ist hier jede Interaktion zwischen Menschen gemeint, die es den Beteiligten erlaubt, ihr Handeln zu koordinieren. Pläne, Tabellen, Zahlen etc. sind sicher Mittel, die im beruflichen Alltag dazu dienen, das Handeln verschiedener Personen zu koordinieren. Jemand erstellt einen Plan eines Hauses; jemand anders schneidet auf Grund dieses Planes Rohre in bestimmte Längen und wieder jemand anders baut diese Rohre auf der Baustelle zu einer Abwasserleitung zusammen. In diesem Sinn kann man daher gut von mathematischer Kommunikation sprechen.

Kommunikation, und damit auch mathematische Kommunikation, ist zielorientiert. Im Beispiel oben wird ein Ziel in der realen, physischen Umwelt angestrebt: Der Aufbau einer funktionierenden Abwasserleitung. Die drei Formen der mathematischen Kommunikation, die Sfard erwähnt, unterscheiden sich danach, welcher Art von Ziel sie dienen:

• Rituale: Bei der Teilnahme an einem mathematischen Ritual ist das Ziel die soziale Akzeptanz durch die Gemeinschaft. Sfard erwähnt als Beispiel ein kleines Kind, das Klötze abzählt. Die Anzahl der Klötze ist ihm unwichtig. Wichtig ist, dass die Erwachsenen ihm bestätigen, dass es richtig gezählt hat.
• Taten: Der Bau der Abwasserleitung bzw. die mathematische Kommunikation in diesem Zusammenhang ist eine mathematische Tat. Wie erwähnt wird hier die Mathematik als Werkzeug genutzt, um ein Ziel in der realen Welt zu erreichen.
• Explorationen: Beim mathematischen Explorieren schliesslich geht es darum, neue mathematische Geschichten zu erzählen. Eine solche Geschichte könnte beispielsweise schlüssig darlegen, dass 3/4 grösser ist als 2/3. Das Ziel ist erreicht, wenn die Gemeinschaft die Darlegung als korrekte mathematische Geschichte akzeptiert.

Alle drei Formen lassen sich so ähnlich im Fachrechnen an Berufsfachschulen beobachten.

Rituale

Aus meiner Sicht ist die Mischrechnung mit dem Mischkreuz ein klassisches Ritual. Bei der Mischrechnung geht es um folgende Fragestellung: Gebraucht werden beispielsweise 200 Liter Milch mit einem Fettgehalt von 2.8%. Zur Verfügung stehen Magermilch mit 0.05% Fettgehalt und Vollmilch mit 3.8% Fettgehalt. Wie viel Milch jeder der beiden Sorten wird für die Mischung benötigt?

Traditionell wird dies über das Mischkreuz berechnet (Abbildung 1).

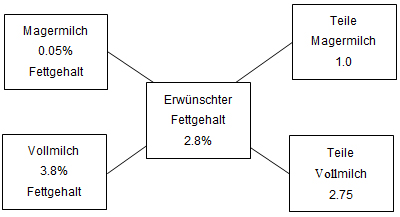
Abbildung 1: Das Mischkreuz

Auf der linken Seite werden die Konzentrationen der beiden Ausgangsprodukte eingetragen. Ins Zentrum kommt die erwünschte Konzentration des Endprodukts. Dann wird „übers Kreuz“ subtrahiert: Rechts wird oben die Differenz zwischen der erwünschten Konzentration und der Konzentration des unteren Ausgangsproduktes eingetragen. Und unten die Differenz der erwünschten Konzentration zur Konzentration des oberen Ausgangsproduktes. Das Verhältnis der beiden errechneten Werte entspricht dem Verhältnis, in dem die beiden Ausgangsprodukte gemischt werden müssen.

Für viele Lernenden ist die Arbeit mit dem Mischkreuz ganz klar die Teilnahme an einem Ritual. Sie vollziehen die magischen Schritte ohne eine Ahnung davon zu haben, was sie hier machen. Ihnen geht es dabei nur um soziale Akzeptanz, beispielsweise in Form einer genügenden Note.

Interessanterweise erfüllt dieses Ritual wie viele Rituale innerhalb der jeweiligen Berufsgruppe eine identitätsstiftende Rolle. Beispielsweise musste im Projekt mit den Milchtechnologen das Mischkreuz explizit in einer Lernumgebung vorkommen, denn etwas überspitzt formuliert, sind die Milchtechnologen ohne das Mischkreuz keine Milchtechnologen mehr.

Selbstverständlich wurde von den Milchtechnologen angeführt, dass das Mischkreuz kein leeres Ritual sei. Man könne mit seiner Hilfe sehr wohl das gesuchte Verhältnis ermitteln. Und folglich sollte man die Verwendung des Mischkreuzes als Tat und nicht als Ritual einstufen.

Dass es sich früher tatsächlich einmal um eine Tat gehandelt hat, lässt sich nicht bestreiten. Zu Zeiten, als es noch keine Taschenrechner und Computer gab, war das Mischkreuz sicher ein sehr nützliches und handliches Werkzeug. Aber heute erledigt ein kleines Computerprogramm die Berechnung schneller und präziser. Das Mischkreuz ist eine ehemalige Tat, die ihren Sinn verloren hat und zum Ritual geworden ist.

Das ist nicht untypisch für Rituale. Auch die zählenden Kinder tun etwas, das in einen anderen Zusammenhang eine Tat sein könnte – die Klötze sind am Schluss im Prinzip gezählt und diese Zahl könnte weiterverwendet werden. Nur steht diese Tat nicht im Zentrum und wird auch nicht bewusst begangen. Typischerweise können kleine Kinder nach dem Ablauf des Zählrituals nicht sagen, wie viele Klötze vor ihnen liegen. Die letzte Zahl beim „Zählen“ hat für sie keine andere Bedeutung, als dass das Ritual abgeschlossen ist. Genauso geht es den Lernenden bei der rituellen Anwendung des Mischkreuzes. Auch sie geben der ermittelten Zahl keine inhaltliche Bedeutung.

Im Hinblick auf die Abzählrituale kleiner Kinder meint Anna Sfard zwar, dass manchmal der Einstieg in die Mathematik nur über die Teilnahme an einem Ritual möglich sei. Das mag für dieses ganz bestimmte Beispiel seine Richtigkeit haben. Werden aber tatsächlich Taten benötigt, ist der Verlass auf Rituale gefährlich. Denn da sie ohne Wissen über ihr Funktionieren ausgeführt werden, gibt es für die Ritualteilnehmer auch keine Möglichkeit zu erkennen, ob das Ritual in der jeweiligen konkreten Berechnungssituation zweckmässig eingesetzt ist und zweckmässig abläuft. Anna Sfard hält dann auch fest, dass man ein Ritual nicht anpassen kann. Treten Schwierigkeiten auf, kann man diese nur beheben, indem man das Ritual in voller Länge nochmals durchspielt (Sfard, 2008, S. 243).

Werkzeuge

Mathematische Taten begehen zu können, d.h. mathematische Werkzeuge bewusst und kontrolliert einzusetzen, setzt voraus, dass Wissen über drei verschiedene Welten zusammenwirkt.

Die Welt der realen Dinge: Um im Beispiel mit der Abwasserleitung Rohre von der richtigen Länge herstellen zu können, muss man einiges über diese Rohre und auch über andere Dinge in der realen Welt wissen. Beispielsweise muss man wissen, dass Kunststoffrohre beim Verschweissen etwas kürzer werden, also etwas länger geplant werden müssen. Bei Metallrohren dagegen muss man einen kleinen Zwischenraum für die Schweissnaht offen lassen, man muss sie also etwas zu kurz planen.

Die Welt der mathematische Zusammenhänge: Die Längen der verschiedenen Rohre lassen sich als Zahlen ausdrücken. Diese Zahlen stehen zueinander in bestimmten Beziehungen, bilden ein mathematisches Modell. Eine einfache solche Beziehung ist, dass die gesamte Länge mehrerer aneinander gereihter Röhren gleich der Summe der einzelnen Längen ist. Etwas weniger einfach ist der Zusammenhang zwischen der Länge der Röhre 3) in Abbildung 2 und den angezeichneten 64 cm.

 

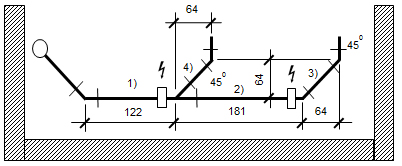
Abbildung 2: Schema einer Abwasserleitung

Die Welt der Rechenverfahren: Mit Hilfe der Zusammenhänge lassen sich aus bekannten Grössen unbekannte Grössen errechnen. Da die Längen aller Teilstücke zusammen die Gesamtlänge ergeben, kann man beispielsweise aus der Gesamtlänge und den bekannten Längen einzelner Teilstücke die unbekannte Länge der fehlenden Röhre errechnen. Das dazu passende Verfahren ist selbstverständlich, dass man von der Gesamtlänge die bekannten Längen subtrahiert.

Eine mathematische Tat wird nur möglich, wenn man bezüglich der sich stellenden Aufgabe in allen drei Welten über genügend Wissen verfügt und wenn man in der Lage ist, dieses Wissen situationsangemessen zu kombinieren. Erst dann funktioniert die Mathematik, die mathematische Kommunikation, wie ein Werkzeug.

Im beruflichen Alltag geht es selbstverständlich oft darum, Mathematik als Werkzeug zu gebrauchen um Taten zu vollbringen. Sei es nun, dass man die passende Länge von Rohren bestimmt, sei es, dass man in der Küche Rezeptangaben von 10 Personen auf 45 Personen umrechnet, sei es, dass eine Pflegende überlegt, wie viele Milliliter eines Medikaments sie aufziehen muss etc.

Diese Integration des notwendigen Wissens zu einem flexiblen Werkzeug können Rituale nicht leisten. Die Ausführung eines mathematischen Rituals spielt sich nur in der Welt der Rechenverfahren ab. Das Resultat hat keinen Bezug zur Welt der realen Dinge. Und die einzelnen Schritte im Ablauf sind nicht mit mathematischen Zusammenhängen hinterlegt und können somit weder sinnvoll angepasst noch überprüft werden.

Beispiele für Mathematik als Werkzeug lassen sich in folgenden Lernumgebungen finden:

Köche

• Rezeptangaben umrechnen – Wie viele Eier muss ich aufschlagen?
• Gefässe wählen – Wie viele Förmchen brauche ich?
• Verlustrechnung – Wie viel muss ich einkaufen/bestellen?
• Warenkosten – Was kosten mich alle benötigten Zutaten?
• Zeitmanagement – Wann muss der Braten in den Ofen?

Haustechniker

• Abwasserinstallation: Rohre in der richtigen Länge vorbereiten für eine verzweigte Abwasserleitung.
• Rohrabstand: Rohre in gleichmässigen Abständen nebeneinander anordnen.
• Heizungsverteiler: Rohre in der richtigen Länge vorbereiten für einen komplexen Aufbau mit Ventilen, Kugelhahnen und Umwälzpumpen.

Explorationsmodelle

Die dritte Kategorie bei Sfard sind Explorationen. Auch diese lassen sich im Kontext des Fachrechnens finden. Beispielsweise wird von Köchinnen und Köchen auf der Stufe EFZ nicht erwartet, dass sie Preisberechnungen ausführen, dass sie also aufgrund von Berechnungen festlegen, welchen Preis sie für den Tagesteller verlangen müssen, um einen bestimmten Gewinn zu machen. Dafür gibt es verschiedene Gründe: Einmal handelt es sich dabei ganz einfach um ein Thema der höheren Fachbildung; auf der Stufe EFZ stehen andere Fragen im Zentrum. Zum zweiten müssten in eine Berechnung dieser Art Angaben einfliessen, die oft nicht genau bekannt sind und durch Annahmen ersetzt werden müssen; eine exakte Kalkulation ist somit gar nicht möglich. Und zum dritten wird vermutlich der Preis eines Tagestellers selten über Berechnungen festgelegt; entscheidender dürfte sein, was die Konkurrenz macht und wie man sich davon abheben kann/will.

Es macht aber trotzdem Sinn, sich im Unterricht damit auseinander zu setzen, was bei der Herstellung eines Tagestellers alles für Kosten anfallen. Tut man das nicht, dann könnte man etwa der Meinung sein, dass es bei einem Tagesteller für 18.- Fr. kaum eine grosse Rolle spielt, ob die benötigten Zutaten zusammen im Einkauf 6.- Fr. oder 8.- Fr. kosten. Die Differenz zwischen Preis und Warenkosten ist in beiden Fällen beträchtlich. Weiss man aber, dass normalerweise die Warenkosten nur etwa 1/3 der anfallenden Kosten ausmachen, sieht die Sache etwas anders aus (Abbildung 3).

Ziel von Explorationen ist es nicht, ganz bestimmte Aufgaben zu lösen (also beispielsweise die exakten Kosten für einen bestimmten Tagesteller zu berechnen), sondern Zusammenhänge zu erkunden: Wenn man die Warenkosten erhöht, wie verändern sich dann die Gesamtkosten? Wenn man den Fettgehalt der Mischung erhöhen will, von welchem Ausgangsprodukt muss man dann mehr nehmen, von welchem weniger? Etc.

Die Nutzung der Mathematik als Modell, um solche Fragen durchzuspielen, ist ebenfalls darauf angewiesen, dass Wissen über die reale Welt und Wissen über mathematische Zusammenhänge in Verbindung gebracht werden, denn schliesslich soll das Modell ja Aussagen über reale Zusammenhänge ermöglichen. Allerdings darf in diesem Fall etwas grosszügiger mit Details umgegangen werden.

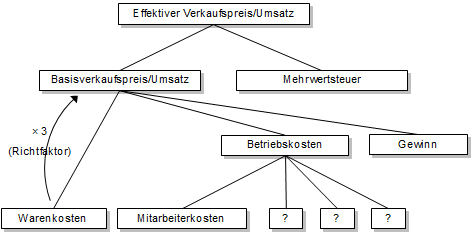
Abbildung 3: Kostenzusammensetzung in der Gastronomie

Beim Erkunden solcher Modelle spielen manchmal auch Rechenverfahren eine Rolle. Aber auch hier genügen oft grobe Näherungen. Es sind keine exakten Berechnungen nötig, um ein Gefühl für die Zusammenhänge zu erhalten.

Beispiele für Mathematik als Explorationsmodell lassen sich in folgenden Lernumgebungen finden:

Köche

• Preiskalkulation – Verdienen wir überhaupt etwas?
• Optimierungsmöglichkeiten – Soll ich ganze Fische bestellen oder Filets?

Rituale, Werkzeuge oder Modelle?

Rituale haben in der Berufsbildung nichts verloren. Was Lernende nur in Form eines Rituals erwerben können, kann immer durch ein kleines Computerprogramm schneller und verlässlicher erledigt werden. Die Lernenden „verstehen“ nicht mehr vom Vorgang, wenn sie die notwendigen Daten anstatt in die Eingabefelder eines Computerprogramms in die Felder des Mischkreuzes eingeben.

Aber natürlich wäre die blinde Benutzung eines Computerprogramms genauso ein Ritual wie das blinde Ausfüllen der Felder des Mischkreuzes. Um ein Computerprogramm als Werkzeug nutzen zu können, braucht es eine Vorstellung der entsprechenden Zusammenhänge: Welche Veränderung ist zu erwarten, wenn ich diese Eingabegrösse verändere? In welcher Grössenordnung wird diese Veränderung sein? Etc.

Die Arbeit mit entsprechenden Modellen liefert hier das notwendige Verständnis. Allerdings eigenen sich die tradierten Rechenverfahren wie das Mischkreuz nicht als Modelle. Sie waren einmal Werkzeuge und sind darauf hin optimiert worden, dass man mit ihnen schnell und ohne viel nachzudenken einen Berechnungsablauf abspulen kann. Andere Formen wie tabellarische Zusammenstellungen mit Hilfe einer Tabellenkalkulationssoftware oder animierte graphische Darstellungen eignen sich hier besser.

Wie erwähnt, setzt das Beherrschen eines Werkzeugs, d.h. das Vollbringen von Taten, voraus, dass man über genügend Wissen in allen drei Welten (reale Dinge, mathematische Zusammenhänge und Rechenverfahren) verfügt und dieses Wissen flexibel und situationsgerecht einsetzen kann. Diesen Punkt zu erreichen ist nicht einfach und braucht einiges an Aufwand. Da die Zeit, in der man mit den Lernenden daran arbeiten kann, typischerweise knapp ist, lohnt es sich daher, immer genau abzuklären, ob wirklich ein Werkzeug erforderlich ist – oder ob man im realen Berufsalltag die Taten nicht besser jemand anderem überlässt (beispielsweise einem Computerprogramm) und sich dafür im Unterricht auf Explorationen mit einem Modell konzentriert.

Erwähnte Literatur

• Kaiser, H. (2009). Modelle bauen und begreifen. Mehr als blindes Rechnen bei angewandten Aufgaben. In L. Hefendehl-Hebeker, T. Leuders & H.-G. Weigand (Eds.), Mathemagische Momente (pp. 74-85). Berlin: Cornelsen.
• Sfard, A. (2008). Thinking as communicating: human development, the growth of discourses, and mathematizing. Cambridge: Cambridge University Press.