pdf    Die im Fachrechnen eingesetzten mathematischen Werkzeuge sind oft das Produkt einer viele Jahre zurückreichenden Tradition. Es lohnt sich, einen kritischen Blick darauf zu werfen. Manchmal ist es möglich, sie durch eine modernere Form zu ersetzen, die als Werkzeug besser in der Hand liegt. Man kann den Lernenden dadurch viel Lernaufwand ersparen und gleichzeitig die Anwendungssicherheit erhöhen.

Verlustrechnung: Von unhandlichen Daten zu handlichen Daten

In der Küche stellt sich folgendes Problem, das in ähnlicher Form auch bei vielen anderen Berufen vorkommt: Werden Karotten geschält, fällt etwas weg, d.h. die geschälten Karotten sind leichter, als es die ungeschälten waren. Wenn ich nun 10 kg geschälte Karotten haben möchte, mit  wie viel Kilogramm ungeschälten Karotten muss ich beginnen?

Verlustprozente

In professionellen Kochbüchern werden als Basis für entsprechende Berechnungen sogenannte „Verlustangaben“ in Prozent publiziert (beispielsweise Pauli, 2010). Auf mehreren Seiten findet man dort Angaben zu „Schälverlusten“, „Entkernverlusten“, „Parierverlusten“ „Garverlusten“ etc.

Beispielsweise verliert man beim Schälen und Putzen folgende Anteile

• Karotten: 15 %
• Erbsen: 50 %
• Kopfsalat: 33 %

Und beim Garen schwindet das Gewicht um folgende Prozentwerte

• Karotten (Dünsten & Glasieren): 30 %
• Spargeln (Sieden): 20 %

Die 10 kg Karotten, die nach dem Schälen übrig bleiben sollen, sind also etwa 85% der ursprünglichen Menge. Und damit man am Schluss wirklich 10 kg hat, muss man folglich mit etwa 11.764 kg beginnen.

Denkt man weiter und möchte man wissen, mit wie viel Karotten man beginnen muss, wenn nach dem Schälen und dem Dünsten & Glasieren noch beispielsweise 8 kg Karotten übrig sind, dann muss dieselbe Rechnung zweimal durchgeführt werden: 8 kg am Ende sind 70% der geschälten Karotten, also braucht es 11.428 geschälte Karotten. Und das wiederum sind 85% der ungeschälten Karotten, also muss man mit 13.445 kg beginnen.

Es sind auch noch mehr Arbeitsschritte denkbar, die zu entsprechend mehr Rechenschritten führen. Beispielsweise bei Gurken: 5% Schälverlust, 20 % Entkernverlust und 12% Tournierverlust.

Faktoren statt Prozente

Eigentlich gibt es im Zeitalter von Smartphones, Computern und Taschenrechnern keinen Grund mehr, solche Berechnungen von Hand durchzuführen. Ein kleines Programm und eine Datenbank erledigen das schneller und präziser.

Will man die Lernenden aber trotzdem so weit bringen, dass sie entsprechende Berechnungen bei Bedarf von Hand durchführen können, kann man sich zumindest überlegen, ob sich das Ganze nicht etwas handlicher gestalten liesse.

Der Frage, die sich aus dem Arbeitsprozess heraus ergibt und die bei diesen Berechnungen beantwortet werden muss, ist immer folgende: Wenn ich am Schluss 60 g Karotten auf dem Teller jedes Gastes haben will, mit wie viel rohen, ungeschälten Karotten muss ich beginnen?

Die publizierten Verlustprozente eigenen sich aber viel besser, um die umgekehrte Frage zu beantworten: Ich habe vor der Bearbeitung 10 kg Karotten. Beim Schälen fallen 15% weg. Also habe ich nach dem Schälen noch 850 g Karotten.

Das lässt sich mit den vorhandenen Angaben recht einfach und ohne grosse Überlegungen beantworten. Nur sind diese Frage und diese Antwort kaum je von Interesse. Für die praktisch relevante Frage hingegen muss man Prozentangaben immer zuerst in mindestens zwei Schritten umformen:

1. Wenn 15% verloren gehen, dann sind die erwünscht 10 kg 85% der Ausgangsmenge.
2. Die Ausgangsmenge ist also 1.176 mal grösser als die Endmenge.

Wie die Verlustprozente ermittelt werden, ist vorstellbar: Man nimmt ein 1 kg Karotten, schält diese und wiegt ab, wie schwer der abgeschälte Teil ist. Warum man aber den Lernenden und überhaupt allen Köchinnen und Köchen zumutet, diese Angaben jedes Mal, wenn sie benötigt werden, umzurechnen, ist nicht nachvollziehbar. Man könnte allen Beteiligten das Leben wesentlich erleichtern, wenn man an Stelle der Verlustprozente direkt die entsprechenden Aufrechnungsfaktoren publizieren würde. Also beispielsweise für Gurken:

• Schälen: 1.052
• Entkernen: 1.250
• Tournieren: 1.136

So wird auf einen Blick sichtbar, dass man, um 10 kg geschälte Gurken zu erhalten, mit 10.520 kg ungeschälter Gurken beginnen muss.

Und will man mehrere Schritte aneinander hängen, genügt es, die entsprechenden Faktoren zu multiplizieren, um einen Gesamtfaktor zu erhalten. Schälen & Entkernen & Tournieren: 1.052 x 1.250 x 1.136 = 1.493.

Mischrechnung: Vom 19. Jahrhundert ins 21. Jahrhundert

Bei der Mischrechnung geht es um folgende Fragestellung: Gebraucht werden beispielsweise 200 Liter Milch mit einem Fettgehalt von 2.8%. Zur Verfügung stehen Magermilch mit 0.05% Fettgehalt und Vollmilch mit 3.8% Fettgehalt. Wie viel Milch jeder der beiden Sorten wird für die Mischung benötigt?

Das Mischkreuz: Ein Werkzeug aus dem 19. Jahrhundert

Traditionell wird dies über das „Mischkreuz“ berechnet.

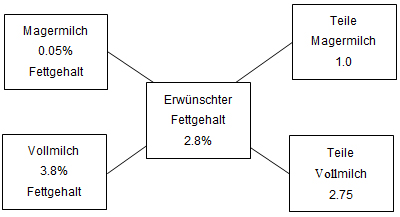
Auf der linken Seite werden die Konzentrationen der beiden Ausgangsprodukte eingetragen (0.05% und 3.8%). Ins Zentrum kommt die erwünschte Konzentration des Endprodukts (2.8%). Dann wird „übers Kreuz“ subtrahiert: Oben rechts wird die Differenz zwischen der erwünschten Konzentration und der Konzentration des unteren Ausgangsproduktes eingetragen (3.8 – 2.8 = 1.0); und untern rechts die Differenz zwischen der erwünschten Konzentration und der Konzentration des oberen Ausgangsproduktes (2.8 – 0.05 = 2.75). Das Verhältnis der beiden errechneten Werte entspricht dem Verhältnis, in dem die beiden Ausgangsprodukte gemischt werden müssen.

Zu Zeiten, als es noch keine Taschenrechner und Computer gab, war dieses Verfahren sicher sehr praktisch. Heute erledigt ein kleines Programm die Berechnung aber schneller und präziser. Es gibt also keinen Grund mehr, das Gehirn Lernender zu Rechenmaschinen umformen zu wollen, zumal sich das Gehirn dafür denkbar schlecht eignet (vgl. dazu etwa Devlin, 2003).

Wenn man sich in der Ausbildung noch mit dem Mischkreuz auseinandersetzt, muss es dafür einen anderen Grund als die praktische Anwendung geben. Und dieser kann eigentlich nur sein, dass man damit bei den Lernenden das Verständnis für die Zusammenhänge zwischen den verschiedenen Grössen fördern möchte. Hier leistet das Mischkreuz aber einen schlechten Dienst. Warum es funktioniert, ist intuitiv nur schwer nachvollziehbar, und entsprechend haben viele Lernende grosse Mühe damit.

Der Sonderfall mit 0%

Dabei sind die Verhältnisse, die sich beim Mischen einstellen, durchaus einem intuitiven Verständnis zugänglich. Werden zwei Teilmengen gemischt, von denen die eine 0% Fettgehalt aufweist, ergibt sich ein besonders übersichtlicher Sonderfall. Der resultierende %-Satz steigt von null ausgehend linear an, je mehr man von der Teilmenge beifügt, deren Fettgehalt von null verschieden ist. Dies lässt sich leicht mittels einer Tabelle durchspielen. Beispielsweise:

Teilmenge I (Fettgehalt 3.8%)	Teilmenge II (Fettgehalt 0%)	Fettgehalt der Mischung
0 Liter	200 Liter	0%
.	.
50 Liter	150 Liter	0.95%
.	.
100 Liter	100 Liter	1.9%
.
150 Liter	50 Liter	2.75%
.	.
200 Liter	0 Liter	3.8%

Eine „Lupe“ für bestimmte Werte

Sucht man das Mischverhältnis für einen bestimmten Zielwert – beispielsweise für 2.5% – kann man den entsprechenden Ausschnitt der Tabelle verfeinern:

Teilmenge I (Fettgehalt 3.8%)	Teilmenge II (Fettgehalt 0%)	Fettgehalt der Mischung
100 Liter	100 Liter	1.9%
.
.	.
125 Liter	75 Liter	2.325%
.	.
137.5 Liter	62.5 Liter	2.5375%
.
150 Liter	50 Liter	2.75%

Mit 137 Liter der Teilmenge I und 63 Liter der Teilmenge II erreicht man vermutlich eine praktikable Näherung. Wie viele Stellen man beim Ausrechnen der Prozentsätze mitschleppen soll, ist eine praktische Frage und hängt davon ab, wie genau das Resultat sein muss.

Der allgemeine Fall

Ist die Konzentration in der Teilmenge II von 0% verschieden, ändert sich nichts Wesentliches. Einzig der Ankerpunkt am unteren Ende der Skala, in der ersten Zeile der Tabelle, ist dann nicht 0% sondern der entsprechende %-Satz für die Konzentration in der Teilmenge II. Beispielsweise:

Teilmenge I (Fettgehalt 3.8%)	Teilmenge II (Fettgehalt 0.05%)	Fettgehalt der Mischung
0 Liter	200 Liter	0.05%
.	.
50 Liter	150 Liter	0.9875%
.	.
100 Liter	100 Liter	1.925%
.
150 Liter	50 Liter	2.8625%
.	.
200 Liter	0 Liter	3.8%

Auch hier gilt: Auf halbem Weg, d.h. wenn von beiden Teilmengen gleich viel eingesetzt wird, ist auch der Prozentsatz auf halbem Weg zwischen dem minimal möglichen und dem maximal möglichen Wert. Etc. Bei einem Zielwert von 2.8% bilden vermutlich 150 Liter und 50 Liter für praktische Zwecke eine ausreichend genaue Näherung.

Eine graphische Variante

Man kann die Aufgabe aber auch graphisch angehen; beispielsweise für den Fall

• gewünschte Menge: 1250 l
• Konzentration in Teilmenge I: 3.5%
• Konzentration in Teilmenge II: 0.3%

Dazu zeichnet man die gewünschte Gesamtmenge (Total) auf der X-Achse und den Fettgehalt der Mischung auf der Y-Achse ein (vgl. Abbildung 1; dort ist der Fettgehalt in Promille angegeben, damit bei der Beschriftung keine Kommas notwendig sind).

Die Menge auf der X-Achse kann man an einer beliebigen Stelle in die beiden Teilmengen TM I (links) und TM II (rechts) unterteilen.

Setzt man den Trennpunkt ganz links, also TM I = 0 und TM II = Total, dann entspricht der Fettgehalt der Mischung natürlich dem Fettgehalt von TM II (im Beispiel Punkt A, ca. 0.3%).

Setzt man den Trennpunkt ganz rechts, also TM I = Total und TM II = 0, dann ist entsprechend der Fettgehalt der Mischung gleich dem Fettgehalt von TM I (im Beispiel Punkt C, ca. 3.5%).

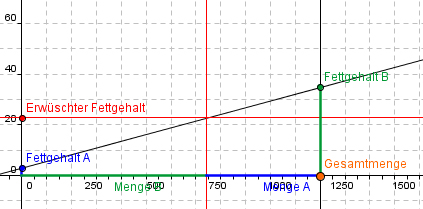
Abbildung 1: Mengenverhältnis und Fettgehalt beim Mischen von zwei Milchmengen.

Für alle Trennpunkte dazwischen liegt der Fettgehalt der Mischung, die so entsteht, auf der Geraden durch die beiden Punkte A und C. Möchte man wissen, welchen Fettgehalt man für eine bestimmte Mischung erhält, kann man einfach vom Trennpunkt nach oben bis zur Graden gehen und dann nach links bis zur Y-Achse (im Beispiel TM I = 740 l, TM II = 510 l, Fettgehalt der Mischung ca. 2.2%).

Natürlich kann man auch umgekehrt von einem gewünschten Fettgehalt auf der Y-Achse über die Gerade zum entsprechenden Trennpunkt gehen und erhält so die benötigten Teilmengen I und II.

Das klassische Mischkreuz lässt sich anhand dieser Darstellung verstehen. Analysiert man, was beim Mischkreuz gerechnet wird, dann sieht man, dass oben rechts und unten rechts je die Differenz zwischen dem erwünschte Fettgehalt und dem Fettgehalt einer der beiden Teilmengen steht. Und das Verhältnis dieser Werte soll offenbar dem Verhältnis der beiden Teilmengen entsprechen – allerdings dem umgekehrten Verhältnis, da die Differenzen ja „übers Kreuz“ gebildet werden. Als Formel geschrieben:

 

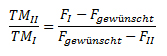
Man kann die Formel auch umschreiben und dann geometrisch interpretieren:

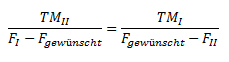
In Abbildung 2 unten sieht man, dass diese vier Grössen die Längen von vier Seiten in zwei Dreiecken sind:

• TM II (Menge A): „Breite“ des rechten Dreiecks
• F I – F gewünscht: „Höhe“ des rechten Dreiecks
• TM I (Menge B): „Breite“ des linken Dreiecks
• F gewünscht – F II: „Höhe“ des linken Dreiecks

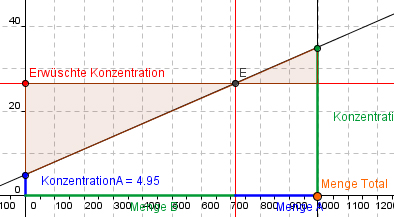
Abbildung 2: Zwei ähnliche Dreiecke beim Mischen von zwei Milchmengen

Diese beiden Dreiecke weisen dieselben Winkel auf, sind also ähnlich. Und dies wiederum bedeutet, dass in den beiden Dreiecken das Verhältnis von „Höhe“ zu „Breite“ gleich gross ist, dass also je die Verhältnisse zwischen der horizontalen Seite (Milchmenge) und der vertikalen Seite (Differenz zwischen zwei Konzentrationen) dieselbe ist. Und das entspricht genau der Aussage der Formel oben und ist somit genau der Zusammenhang, der im klassischen Mischkreuz genutzt wird.

Eine kleine Animation

Im 21. Jahrhundert kann man die Graphik natürlich auch bewegt darstellen. Ich habe dazu mit GeoGebra eine kleinen Animation entworfen. (Sollte die Animation nicht laufen, kann man die GeoGebra Datei auch herunterladenund lokal mit GeoGebra ausführen.)

Will man diese Animation in der Ausbildung oder gar im beruflichen Alltag nutzen, müsste man sie noch etwas sorgfältiger ausbauen. Beispielsweise lässt sich der Trennpunkt im Moment noch nach links und rechts unter null bzw. über die Totalmenge hinaus verschieben, was natürlich nicht sein darf. Vermutlich liesse sich die Animation mit wenig Aufwand als App für Smartphones realisieren.

Zitierte Literatur

• Devlin, K. (2003). Das Mathe-Gen: oder Wie sich das mathematische Denken entwickelt + Warum Sie Zahlen ruhig vergessen können. München Deutscher Taschenbuch Verlag.
• Pauli, P. (2010). Lehrbuch der Küche. Neuhausen a.R.: Pauli Fachbuchverlag.