pdf    Im beruflichen Alltag spielen einfache Proportionalitätsüberlegungen eine grosse Rolle: Wenn doppelt so viele Gäste kommen, muss ich doppelt so viel Reis kochen; wenn die Spannung doppelt so gross ist, fliesst doppelt so viel Strom; wenn ich heute nur ein Stockwerk an Stelle von zwei reinigen muss, sollte ich in der Hälfte der Zeit fertig sein.

All diese Zusammenhänge lassen sich elegant und knapp als Formel darstellen. Einige dieser Formeln haben es dabei sogar zu einer gewissen Berühmtheit gebracht, so etwa U=R×I für den Zusammenhang zwischen Strom und Spannung.

Formeln sind aber eine Art stenographische Notation. Es braucht viel Routine, um damit arbeiten zu können, um beispielsweise zu sehen, welchen Einfluss die Veränderung einer Grösse auf andere Grössen hat (Devlin, 2012). Alternativ lassen sich jedoch proportionale Zusammenhänge auch als Tabellen darstellen. Und diese Art der Darstellung eignet sich besser für den alltäglichen Gebrauch.

Nursing Rule

Ein Beispiel dafür stammt aus einer Untersuchung aus England: Im Rahmen eines Forschungsprojektes wurden Pflegende in einem Kinderspital beobachtet, wie sie eine Infusion vorbereiteten (Hoyles, Noss, & Pozzi, 2001). Wie üblich hatte der Arzt oder die Ärztin festgelegt, wie viel Milligramm eines Wirkstoffs ein bestimmtes Kind erhalten sollte – beispielsweise 180 mg. Zur Verfügung standen standardisierte Packungen, die jeweils 120 mg Wirkstoff gelöst in 10 ml Flüssigkeit enthielten. Die Pflegenden mussten sich beim Vorbereiten der Infusion also überlegen, wie viele Packungen sie benötigten, um die vorgegebene Menge Wirkstoff zu erreichen.

Natürlich kann man diesen Zusammenhang mit Hilfe einer Formel darstellen. Etwa so:

• a: Wirkstoffmenge in der Standardpackung (mg)
• b: Volumen der Standardpackung (ml)
• c: Verordnete Wirkstoffmenge (mg)
• d: Benötigtes Volumen (ml)

Selbstverständlich könnte man diese Formeln nun nutzen, um jede beliebige der vier Grössen aus den restlichen drei zu errechnen. Da im Berufsalltag aber immer dieselbe Grösse gefragt ist – das benötigte Volumen – wird in England in den Schulen die Formel nach dieser Grösse aufgelöst gelehrt:

Bekannt ist diese Formel als nursing rule. Mit den Zahlen des Beispiels:

Der Unterricht in den Berufsfachschulen trägt also dem Umstand Rechnung, dass von den potentiell möglichen vier Rechenaufgaben im beruflichen Alltag real nur eine auftritt. Und mit der Wahl der Begriffe wird versucht, eine direkte Verbindung zu dieser Situation herzustellen. Sowohl Lehrenden wie auch Vorgesetzte im Spital bestätigten den Forschern auf Anfrage, dass die Berechnung mit Hilfe dieser Formel die Methode sei, mit der die Aufgabe im Alltag professionell gelöst würde.

Die Forscher beobachteten anschliessend Pflegende im Berufsalltag um zu sehen, wie diese wirklich vorgehen. Und dabei zeigte sich, dass die wenigsten Pflegenden zu Papier und Bleistift oder dem Taschenrechner greifen und die Formel einsetzen. Vielmehr schienen sie ausgehend von dem Zahlenpaar auf der Packung (z.B. 120 mg in 10 ml) vor ihrem inneren Auge das Bild von zwei parallelen Skalen zu bilden; etwa wie folgt:

120 mg	10 ml
60 mg	5 ml
30 mg	2.5 ml
6 mg	0.5 ml
3 mg	0.25 ml

Wird nun beispielsweise eine Dosis von 30 mg verlangt, wandern sie auf beiden Skalen gleichzeitig in die entsprechende Richtung. Dabei machen sie rechnerisch einfach zu bewältigende Sprünge, also z.B. von 120mg/10ml zu 60mg/5ml (halbieren) und dann zu 30mg/2.5ml (nochmals halbieren). So können sie schnell und mit grosser Sicherheit die jeweils benötigte Flüssigkeitsmenge bestimmen.

Dieses Alltagswerkzeug hat gegenüber der nursing rule verschiedene Vorteile. Vor allem ist sein Gebrauch viel weniger fehleranfällig. Dasselbe innere Bild von „Milligramm Wirkstoff gelöst in Milliliter Flüssigkeit“ bleibt während des ganzen Vorgangs erhalten. Es kommt zu keinen Zwischenresultaten (wie nach dem Dividieren bei der nursing rule), die schwierig zu interpretieren sind. Es entstehen daher kaum unentdeckte Rechnungsfehler. Und schon gar keine wirklich gefährlichen, wie sie beim Rechnen nach der nursing rule auftreten können, wenn man sich beispielsweise beim Dividieren um eine Kommastelle vergreift und plötzlich das Zehnfache des richtigen Wertes erhält. Entsprechend beobachteten die Forscher in über 80 Situationen auch keine Fehler, obwohl die benötigten Mengen alle im Kopf berechnet wurden.

Milchtechnologen

In der modernen Mathematikdidaktik ist es nicht unüblich, proportionale Zusammenhänge in Form von Wertetabellen als „parallele Skalen“ zu behandeln. In vielen Lehrmitteln findet man Aufgaben der folgenden Art:

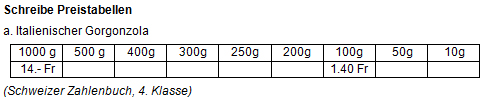
Das Interessante am Vorgehen der Pflegenden ist aber, dass die Tabelle nicht dazu dient, um darauf aufbauend die nursing rule zu lernen oder um die nursing rule zu üben. Die Tabelle bzw. das Bild der parallelen Skalen ist das mathematische Instrument der Wahl, das im beruflichen Alltag eingesetzt wird.

Aus der Forschung weiss man auch, dass Lernende auf der Sekundarstufe I, wenn sie mit solchen Instrumenten arbeiten, deutlich weniger Fehler machen, als wenn sie Formeln einsetzen. In einer Untersuchung wurden bei Einsatz von Formeln nur 30% der Aufgaben richtig gelöst. Beim Einsatz andere Instrumente gab es hingegen 80% richtige Lösungen (Hafner, 2012).

Ein Grund dafür dürfte sein, dass beim Arbeiten mit parallelen Skalen keine Zwischenresultate entstehen, die nicht interpretiert werden (können) – wie etwa das Resultat nach der Division bei der nursing rule.

Man kann solchen „Zwischengrössen“ eine Interpretation als „Proportionalitätsfaktor“ geben: Im Arbeitsalltag der Milchtechnologen ist es typischerweise so, dass die angelieferte Milch in Liter gemessen, aber später dann in Kilogramm abgerechnet wird. Daher muss irgendwann die Milchmenge von Liter in Kilogramm umgerechnet werden. Auch dieser Zusammenhang lässt sich als Formel darstellen:

m = d x V

• V: Volumen der angelieferten Milch (l)
• d:  Dichte der Milch (kg/l)
• m: Masse der angelieferten Milch (kg)

Der hier relevante Proportionalitätsfaktor, die Dichte, hat also sogar einen Namen. Allerdings haben die Lernenden erfahrungsgemäss trotzdem enorm Mühe, sich darunter etwas vorzustellen. Dies äussert sich unter anderem darin, dass sie sich die mit der Dichte verbundenen Masseinheiten nicht merken können.

Auch hier erlaubt die Formel im Prinzip aus jeweils zwei Angaben die dritte zu berechnen. Im beruflichen Alltag tritt aber nur eine dieser Möglichkeiten auf, nämlich die Umrechnung von Volumen in Masse. Und auch das lässt sich gut als parallele Skalen handhaben und in Form einer Tabelle darstellen:

Liter	kg
1	1.030
100	103
1000	1030
.

Um mit dieser Berechnungssituation umgehen zu können, müssen angehenden Milchtechnologen so einfach wissen, wie schwer ein Liter Milch ist. Diese Information in der ersten Zeile der Tabelle verankert die beiden Skalen gegenseitig. Die anderen Zeilen ergeben sich daraus ohne weiteres und viele Werte können problemlos im Kopf generiert werden.

Diese Darstellung und dieses Vorgehen haben den Vorteil, dass sie das Ganze auf das in der Anwendungssituation Wesentliche reduziert. Die „Dichte“ erhält eine kontextbezogene konkrete Interpretation: Das Gewicht eines Liters Vollmilch. Dass diese Angabe in der Physik „Dichte“ genannt wird, ist in diesem Kontext irrelevant. (Auch wenn es im Rahmen der beruflichen Grundbildung im Hinblick auf allgemeinbildende Ziele behandelt werden kann und soll.)

Tabellen als mathematisches Modell und Werkzeug bei einfacher Proportionalität

Um mit Tabellen zu arbeiten, eignen sich vor allem einmal einfache proportionale Zusammenhänge im Sinne der erwähnten Beispiele: „Wenn ich das hier verdopple, muss ich auch jenes dort verdoppeln“. Tabellen dieser Art lassen sich besonders einfach interpolieren und erweitern. Beispiele, die irgendwo in einem beruflichen oder privaten Handlungskontext eine Rolle spielen, gibt es viele:

• Preis und Menge: Ein Stück kostet 2.50 Fr.; zwei Stück …; zehn Stück …
• Prozente: 10% Rabatt sind 11.- Fr.; 20% …; 40% …
• Zutaten und Anzahl Portionen: Für 4 Personen 300 g Reis; für 2 Personen …; für 10 Personen …
• Farbe und Fläche: 1 Kübel für 12 m²; 2 Kübel für …; 5 Kübel für …
• Euro und Franken: 1 Euro kostet 1.25 Fr; 20 Euro …; 100 Euro …
• Distanz und Zeit: Für 60 km eine Stunde; für 30 km …; für 90 km …
• Flaschen und Packungen: In einer Packung 6 Flaschen; in 2 Packungen …; in 3 Packungen …
• Benzinverbrauch und Distanz: Für 100 km 6 Liter; für 125 km …; für 50 km …

Allen diesen Beispielen gemeinsam ist, dass sie als Ausgangspunkt ein Verhältnis haben, das durch den Kontext gegeben ist (Art der Packung, Art des Fahrzeugs, aktueller Wechselkurs, Angaben im Kochbuch etc.). Dieses kann in einer tabellarischen Darstellung als Ankerzeile genutzt werden, von der aus andere „Zeilen“ exploriert werden können:

	Euro	Franken
	0.50
Ankerzeile	1	1.25
		2.50

Diese Exploration kann in vier Richtungen erfolgen: In jeder Spalte sowohl nach unten wie nach oben. Häufig führen dabei Verdoppeln oder Halbieren der Werte zu neuen nützlichen Wertepaaren.

Hier ein Beispiel aus einer Lernumgebung für die Ausbildung zum Gärtner/zur Gärtnerin:

Erfahrungsgemäss sind die Lernenden beim Bearbeiten solcher Aufgaben sehr erfinderisch und wählen unterschiedlichste Strategien, bei denen sie sich wohl fühlen. Eine Lehrende berichtet:

„Mit dem Instrument parallele Skalen liessen sich alle Aufgaben mit einer praxistauglichen Genauigkeit lösen. Wo sie genauer sein wollten, haben die Lernenden nach einigem Herumprobieren anhand der Tabellen auch auf 1 Einheit zurückgerechnet, um sie anschliessend mit dem gesuchten Wert zu multiplizieren. Und so den Dreisatz entdeckt! Und sofort wieder vergessen!

Diese Situation hat sich mehrfach wiederholt. Ich habe den Lernenden zwar jeweils kurz erklärt, dass sie soeben den Dreisatz entdeckt hätten und sich so jede der gestellten Aufgaben ganz schnell lösen lasse. Das hat sie aber nicht weiter interessiert und ich habe nicht insistiert. Es schien mir wichtiger, dass die Lernenden den Spass am Rechnen mit parallelen Skalen auskosten können, als ihnen Neues zu zeigen, das sie als Belastung empfinden.

Die Lernenden haben das Rechnen mit den parallelen Skalen intuitiv erfasst und hatten Spass daran, auch neue Tabellen auszufüllen.“

Für Anspruchsvolle (1): Zusammenhänge zwischen mehr als zwei Grössen

Tabellarische Werkzeuge lassen sich auch auf Zusammenhänge zwischen drei oder mehr Grössen ausdehnen. Hier ein Beispiel für den Farbverbrauch beim Malen:

	Länge (m)	Breite (m)	Fläche (m2)	Farb- eimer (Anzahl)
Ankerzeile	4	3	12	1
	2		12	1
	8			1
		6		1
		9		1
	4	6

Die Ankerzeile hat in diesem Fall eine etwas andere Form als bisher. Sie beschreibt eine mögliche Form eines Wandstücks, welches sich mit einem Eimer Farbe überstreichen lässt. Andere Formen mit derselben Fläche lassen sich daraus durch „Strecken“ und „Kürzen“ gewinnen. Gleichzeitig ist noch eine vierte Grösse, die Anzahl Eimer, erfasst. Verändert man die Grösse der Fläche, ändert sich natürlich Anzahl Eimer entsprechend.

Spannend ist folgende Tabelle, die im Unterricht für Elektromonteure zum Einsatz kommt und ebenfalls zwei Zusammenhänge vereint.

U = R x I    und     P = U x I

Als Ankerzeile sind Werte in einer Grössenordnung eingefügt, wie die Elektromonteure sie in ihrem normalen Berufsalltag antreffen (1A und 230V). Die Tabelle entspricht den üblichen Fragestellungen aus diesem Berufsalltag: Die Spannung ist gegeben (im Haushaltsbereich 230V) und ein Verbraucher mit einer bestimmten Leistung wird angeschlossen. Welcher Strom fliesst und muss abgesichert werden?

	P	R	I	U
Ankerzeile	230 W	230ohm	1A	230V
	60W			230V
	2000W			230V
			2A	230V
		500ohm		230V
			10A	 230V

Für Anspruchsvolle (2): Allgemeine lineare Zusammenhänge

In den bisherigen Beispielen war es immer so, dass wenn eine Grösse gleich Null war, die andere Grösse ebenfalls Null wurde: 0 Liter Milch wiegen 0 Kilogramm; 0 Euro kosten 0 Franken; für 0 m² Wiese braucht es 0 kg Dünger etc. Es gibt aber auch lineare Zusammenhänge zwischen zwei Grössen, bei denen dies nicht der Fall ist. Beispielsweise entsprechen 0° Celsius nicht 0° Fahrenheit sondern 32° Fahrenheit.

Bei solchen Zusammenhängen wird das Arbeiten mit Tabellen zwar etwas komplexer, es ist aber durchaus noch machbar und sinnvoll. Beispiele für solche Zusammenhänge lasen sich ebenfalls viele finden:

• Temperatur in Grad Celsius und in Grad Fahrenheit
• Stromkosten zusammengesetzt aus einem Grundbetrag und einer verbrauchsabhängigen Komponente
• Fahrzeugkosten zusammengesetzt auf Fixkosten und variablen Kosten
• Der Fettgehalt einer Mischung aus zwei Milchsorten
• …

	Celsius	Fahrenheit
	.
Ankerzeile 1	0	32
	10
Ankerzeile 2	20	 68
	.

Für solche Fälle werden zwei Ankerzeilen benötigt. (Im Fall der einfachen Proportionalität bildet das Paar (0,0) die zweite Ankerzeile.) Die Interpolation zwischen diesen beiden Zeilen ist einfach zu bewerkstelligen: Liegt ein Wert auf der einen Skala in der Mitte zwischen den beiden Ankerzeilen, so liegt der entsprechende Wert auf der anderen Skala auch in der Mitte.

Ein spannendes Beispiel für den Einsatz von Tabellen dieser Art ist die Mischrechnung. Dabei geht es beispielsweise (auch wieder bei den Milchtechnologen) um folgende Frage: Gebraucht werden 800 Liter Milch mit einem Fettgehalt von 2%. Zur Verfügung stehen Magermilch mit 0.05% Fettgehalt und Vollmilch mit 3.5% Fettgehalt. Wie viel Milch jeder der beiden Sorten wird für die Mischung benötigt?

Traditionell wird dies über das „Mischkreuz“ berechnet. Dabei wird folgender Zusammenhang genutzt.

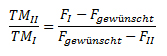
Umgangssprachliche formuliert: Das Verhältnis der beiden Mengen entspricht dem umgekehrten Verhältnis der Differenzen zwischen den jeweiligen Fettgehalten und dem gewünschten Fettgehalt. Das ist intuitiv kaum nachvollziehbar und Lernende haben traditionell auch grosse Mühe mit diesem Zugang.

Dabei liegt dem Ganzen ein einfacher linearer Zusammenhang zu Grunde. Verwenden man für die Mischung nur Milch der einen Sorte, dann entspricht selbstverständlich der Fettgehalt der „Mischung“ dem Fettgehalt dieser Sorte. Damit sind die beiden Ankerzeilen der folgenden Tabelle gegeben. Alle anderen Werte dazwischen lassen sich linear interpolieren. Speziell an dieser Tabelle ist, dass nur zwischen den beiden Ankerzeile interpoliert werden kann. Eine Extrapolation darüber hinaus ist sinnlos.

	Vollmilch (Liter)	Magermilch (Liter)	Fettgehalt total
nur Magermilch	0	800	0.05%
	.	.
	200	600
	.	 .
	400	400
	.
	600	200
	.	 .
nur Vollmilch	800	0	3.5%

Formeln als elegante Zusammenfassungen von Tabellen

Im privaten und beruflichen Alltag genügt im Allgemeinen das Arbeiten mit parallelen Skalen den dort herrschenden Anforderungen – allenfalls unterstützt von tabellarischen Darstellungen. Lernende, die nicht darüber hinausgehen wollen oder können, können trotzdem erfolgreiche Berufsleute werden.

Es spricht aber nichts dagegen, anschliessend an die Behandlung der Zusammenhänge in tabellarischer Form, Formeln als elegante Zusammenfassungen von Tabellen zu thematisieren. Vorausgesetzt ist natürlich, dass im Unterricht entsprechend Zeit vorhanden ist. V.a. bei Lernende, die später evtl. die Berufsmaturität oder eine höhere Weiterbildungen absolvieren möchten, ist es gut, wenn sie sich damit auseinandersetzen.

Alle bisher aufgeführten Beispiele eignen sich dafür. Dazu sind drei Schritte nötig:

1. Abstrahierende Beschriftung der Kolonnen
2. Einführen/Einfügen eines Proportionalitätsfaktors
3. Ausformulieren des Bezugs zwischen den Grössen als Formel

Im Fall des Zusammenhangs zwischen Masse und Volumen bei den Milchtechnologen könnte das beispielsweise so aussehen:

		Faktor
abstrahierende Beschriftung	Volumen V	Dichte d	Masse m
	Milch (Liter)	kg/l	Milch (kg)
	1	1.032	1.032
	100	1.032	103.2
	1000	1.032	1032

Bezug zwischen den Grössen

V

x

d

=

m

Wichtig ist dabei, dass das Darstellen der Zusammenhänge als Formel nicht mit dem Betreiben von Mathematik verwechselt wird. Keith Devlin hat in seinem Buch „Das Mathe-Gen“ für die Funktion von Formeln eine schönes Bild gefunden (Devlin, 2003). Er vergleicht Mathematik betreiben mit Musik machen. Beides findet im Kopf satt. Die Musiker haben die Notenschrift entwickelt, um das darstellen zu können, was beim Musik machen im Kopf stattfindet. Zum selben Zweck haben die Mathematiker die Formeln erfunden. Beides sind statische Zusammenfassungen von dynamischen Denkprozessen.

Komplexe Mathematik kann man kaum ohne das Hilfsmittel der Formeln betreiben. Die Mathematik, welche im beruflichen Alltag benötigt wird, meist aber schon. Und wie man nicht zwingend Noten lesen können muss, um Musik zu machen, muss man nicht zwingend „Formeln lesen“ können, um Mathematik zu betreiben.

Zitierte Literatur

• Devlin, K. (2003). Das Mathe-Gen: oder Wie sich das mathematische Denken entwickelt + Warum Sie Zahlen ruhig vergessen können. München Deutscher Taschenbuch Verlag.
• Devlin, K. (2012). The Symbol Barrier of Mathematics Learning. In M. Bockarova, M. Danesi & R. Núñez (Eds.), Semiotic and Cognitive Science Essasy on the Nature of Mathematics (pp. 7-16). München: LINCOM.
• Hafner, T. (2012). Proportionalität und Prozentrechnung in der Sekundarstufe I. Wiesbaden: Vieweg + Teubner.
• Hoyles, C., Noss, R., & Pozzi, S. (2001). Proportional Reasoning in Nursing Practice. Journal for Research in Mathematics Education, 32(1), 4-27.

Tools

• Skalenrechner