etwas ausführlicher als pdf

Situierte Kompetenz

Kompetenz gleich welcher Art ist situationsgebunden. Wenn eine Person eine bestimmte Situation kompetent bewältigen kann, ist damit noch lange nicht gesagt, dass ihr dies in einer anderen, vermeintlich ähnlichen Situation ebenfalls gelingt. Dies gilt auch für Berechnungssituationen jeglicher Art. Eine kleine Geschichte als Beispiel, erzählt von Hans Heymann, Mathematikdidaktiker (Heymann, 1996, S. 207f; das Zitat ist leicht gekürzt):

„Eine charakteristische Szene mit meiner Tochter Katharina – seinerzeit 13 Jahre alt und dem Fach Mathematik nicht sonderlich zugetan – erlaubt Vermutungen darüber, durch welche Missverständnisse die Kluft zwischen dem mathematischen Denken und dem Alltagsdenken zustande kommt: Katharina hatte, im Rahmen einer Hausaufgabe, unter ordnungsgemässer Anwendung der Bruchrechenregeln die Zahl 2 durch ¼ dividiert und kam dann zu mir, weil sie sich über die 8 als Ergebnis wunderte. Wieso konnte das Ergebnis grösser sein als der Dividend? Sie hatte doch ‚geteilt’! Ich versuchte ihr einsichtig zu machen, weshalb das so sein muss. Als Gegenbeispiel hielt sie mir vor, wenn sie einen Apfel ‚in Viertel’ teile, seien die Stücke aber kleiner als der Apfel. Ich wies sie auf den Unterschied zwischen ‚teilen in’ und ‚teilen durch’ hin. Abschliessend meinte sie: ‚Okay, ich weiss jetzt, wie man das rechnen muss. Aber du willst mir doch wohl nicht weismachen, dass man in Mathe logisch denkt!’“

Mit dieser Schwierigkeit steht Katharina nicht allein da. Nach meinen persönlichen Schätzungen bekommen mindestens die Hälft aller Leute das Dividieren durch einen Bruch nie in den Griff – unabhängig vom Bildungsniveau. Das Problem ist, dass sie eine ganz bestimmte Situation vor Augen haben: Das „Teilen“ oder „Verteilen“ eines Apfels oder Kuchens auf mehrere Kinder. Daneben gibt es aber noch andere Situationen, die man zwar auch mit Dividieren bewältigen kann, die aber einer ganz anderen Fragestellung entsprechen.

Eine typische zweite solche Situation wäre das „Aufteilen“ oder „Enthaltensein“. Beispielsweise: „2 kg Mehl sollen in Säcke zu ¼ kg abgefüllt werden. Wie viele Säcke benötigt man?“ Für die meisten Personen verschwinden ihre ursprünglichen Probleme augenblicklich, wenn sie sich diese Situation vorstellen. Die Aufgabe wird leicht lösbar. Und in diesem Kontext bereitet es überhaupt keine Mühe zu akzeptieren, dass das Resultat (8) grösser ist, als die Anzahl Kilogramm in der Ausgangsmenge.

Aus der Forschung weiss man, dass sich im Zusammenhang des Dividierens eine Vielzahl solcher Situationen unterschieden lassen. Jeder dieser Situationen liegt eine andere Sachlogik zugrunde. So ruft z.B. „Ein Teppich ist 20 m² gross. Er ist 4 m breit. Wie lang ist er?“ wieder ein ganz anders Bild hervor als das Verteilen eines Kuchens auf mehrere Personen oder das Aufteilen eines Sack Mehls auf mehrere kleine Säcke.

All diese Sachverhalte kann die „abstrakte Mathematik“ durch dasselbe mathematische Konzept – der Division einer Grösse durch eine andere – darstellen und behandeln (vgl. Abbildung 1). Aber damit allein lässt sich im Alltag eine entsprechende Aufgabe nicht schnell und sicher lösen. Unter anderem braucht es dazu eine Vorstellung davon, was in der Situation tatsächlich geschieht (vgl. etwa Vergnaud, 1990). Eine solche Vorstellung hilft etwa abzuschätzen, ob das Resultat überhaupt stimmen kann. Erhält man z.B. beim Verteilen von Äpfeln an Kinder pro Kind mehr Äpfel als ursprünglich zur Verfügung standen, dann muss etwas schief gegangen sein.

Dass Kompetenz im Sinne von „eine Berechnungssituation sicher und effizient beherrschen“ situationsgebunden ist, erkennt man gut, wenn man kompetente Leute danach fragt, ob das Resultat einer bestimmten Berechnung zutreffen kann. Je nach Situation erhält man ganz andere Begründungen:

• Vier Kinder teilen sich zwei Äpfel: Dies ergibt einen Apfel auf je zwei Kinder, also einen halben Apfel pro Kind.
• 2 kg Mehl sollen in Säcke zu ¼ kg abgefüllt werden: Für ein Kilogramm braucht es vier Säcke, also insgesamt 8 Säcke.
• Ein Teppich ist 20 m² gross. Er ist 4 m breit: Wenn man sich den Teppich in der Längsrichtung vor sich liegend vorstellt, dann hat vorne eine Reihe von vier Quadratmetern Platz. Dahinter kann eine weitere Reihe hingelegt werden usw. Insgesamt haben fünf solche Reihen Platz, also ist der Teppich fünf Meter lang.

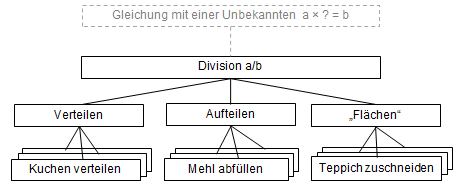
Abbildung 1: Verteilen und Aufteilen und andere Spezialfälle des Dividierens

„Dividieren können“ ist also als allgemeine mathematische Kompetenz ein hoch gestecktes Ziel. Um von einer derartigen Kompetenz sprechen zu können, muss eine Person einerseits in einer Vielzahl von gängigen Situationen je über eine entsprechende situative Kompetenz verfügt. Zum anderen muss sie, wenn eine neue, noch unvertraute Situation auftaucht, in der Lage sein, sich schnell in deren Eigenarten hineinzudenken. Wer das kann, hat natürlich einen Vorteil. Für viele ist dies aber ein zu hoch gestecktes Ziel – zu hoch, für das, was sie erreichen können und/oder wollen, aber auch zu hoch, für das, was sie erreichen müssen, um im (beruflichen) Alltag zurechtzukommen.

Abstrakte und weniger abstrakte Werkzeuge

Dividieren

Die verschiedenen Ebenen in Abbildung 1 können als immer abstraktere und dadurch vielseitigere Werkzeuge verstanden werden, mit denen sich eine immer grössere Menge konkreter Aufgaben bearbeiten lässt. Diese Pyramide lässt sich nach oben ohne weiteres noch um einige Stufen erweitern. Man kann die Division a/b wiederum als einen Spezialfall eines noch viel mächtigeren Werkzeugs verstehen, nämlich das Auflösen einer Gleichung mit einer Unbekannten (Abbildung 1).

Jede dieser Ebenen hat ihre Berechtigung. Entscheidend ist, dass man je nach Zielgruppe für die Lernenden jenes Werkzeug wählt, welches sie beherrschen können.

Dreisatz

Im Rahmen eines Forschungsprojektes wurden Pflegende in einem Kinderspital beobachtet, wie sie eine Infusion vorbereiteten (Hoyles, Noss, & Pozzi, 2001). Wie üblich hatte der Arzt oder die Ärztin festgelegt, wie viel Milligramm eines Wirkstoffs ein bestimmtes Kind erhalten sollte – beispielsweise 180 mg. Zur Verfügung standen standardisierte Packungen, die beispielsweise jeweils 120 mg Wirkstoff gelöst in 10 ml Flüssigkeit enthielten. Die Pflegenden mussten sich beim Vorbereiten der Infusion überlegen, wie viele Packungen sie benötigten, um die vorgegebene Menge Wirkstoff zu erreichen.

Mathematisch abstrakt gesprochen steht bei dieser Situation eine „Proportion“ im Zentrum: „Eine Packung enthält 120 mg Wirkstoff. Wie viele Packungen enthalten 180 mg Wirkstoff?“ Als allgemeines Werkzeug bietet sich ein „Dreisatz“ an. Entsprechend hatten die Pflegenden in der Ausbildung die sogenannte „nursing rule“ kennengelernt, die übersetzt etwa wie folgt lautet:

Mit den Zahlen des Beispiels

Die Beobachtungen zeigten nun aber, dass dieses Werkzeug im Berufsalltag selten gebraucht wurde. Die wenigsten Pflegenden griffen zu Papier und Bleistift oder zückten den Taschenrechner. Stattdessen gelangte meist folgende Strategie zur Anwendung:

Ausgehend von dem Zahlenpaar auf der Packung (z.B. 20 mg in 10 ml) bildeten die Pflegenden vor ihrem inneren Auge das Bild von zwei parallelen Skalen; etwa wie folgt:

120 mg	10 ml
60 mg	5 ml
30 mg	2.5 ml
6 mg	0.5 ml
3 mg	0.25 ml

Wurde nun z.B. eine Dosis von 30 mg verlangt, sprangen sie auf beiden Skalen gleichzeitig in die entsprechende Richtung. Dabei machten sie rechnerisch einfach zu bewältigende Sprünge, also z.B. von 120mg/10ml zu 60mg/5ml (halbieren) und dann zu 30mg/2.5ml (nochmals halbieren). So konnten sie schnell und mit grosser Sicherheit die jeweils benötigte Flüssigkeitsmenge bestimmen.

Diese Alltagsstrategie hat gegenüber der „nursing rule“ den Vorteil, dass sie viel weniger fehleranfällig ist. Dasselbe innere Bild von „Milligramm Wirkstoff gelöst in Milliliter Flüssigkeit“ bleibt während des ganzen Vorgangs erhalten. Es kommt zu keinen Zwischenresultaten (wie nach dem Dividieren bei der „nursing rule“), die schwierig zu interpretieren sind. Es entstehen dadurch kaum unentdeckte Rechnungsfehler. Und schon gar keine wirklich gefährlichen, wie sie beim Rechnen nach der „nursing rule“ auftreten können, wenn man sich beispielsweise beim Dividieren um eine Kommastelle vergreift und plötzlich das Zehnfache des richtigen Wertes erhält.

Ähnlich wie beim Dividieren lässt sich also auch hier eine Hierarchie von immer abstrakteren Konzepten für Problemstellungen finden, die mit einem „Dreisatz“ angegangen werden können:

• Am einfachsten sind parallele Skalen, h. graphische Darstellungen oder mentale Vorstellungen, die es erlauben, gekoppelte Grössen im Gleichschritt zu variieren.
• Ein etwas mächtigeres Werkzeug ist dann der eigentliche Dreisatz – die zwei Schritte von a Einheiten zu einer Einheit und dann von einer Einheit zu b Einheiten.
• Noch vielseitiger ist das Konzept von zwei gleichen Proportionen (das dann auch gleich neu die Idee der „umgekehrten“ Proportionalität ins Spiel bringt)
• Und all diese Konzepte lassen sich wieder als Spezialfall einer Gleichung mit einer Unbekannten

Situierte und abstrakte Werkzeuge

Die Beispiele zeigen, dass die Mathematik als Disziplin zwar viele mächtige und vielseitig anwendbare Werkzeuge anbietet. Die abstrakteren davon sind aber nicht unbedingt für den alltäglichen, praktischen Einsatz geeignet. Das Verhältnis zwischen dem Einsatz abstrakterer mathematischer Werkzeuge und der Bewältigung beruflicher Berechnungssituationen ist ähnlich wie das Verhältnis zwischen dem Programmieren und dem Benutzen eines Computers. Möchte man jemanden lehren, wie man am Computer eine Fussnote in einen Text einsetzt, so kann man dieser Person natürlich zu diesem Zweck das Programmieren beibringen. Denn mit Programmieren lässt sich grundsätzlich jede Aufgabe lösen, die sich am Computer stellt. Nur ist der Weg über das Programmieren weit und anspruchsvoll. Anstatt über Datenstrukturen und logischen Verzweigungen spricht man daher besser darüber, in welchem Menü des benutzten Programms sich der Befehl zum Einfügen der Fussnote befindet.

Ähnliches gilt für die Mathematik. Für viele berufliche aber auch alltägliche Situationen gibt es robuste situierte mathematische Werkzeuge (dazu etwa van der Kooij, 2001). Deren Beherrschung gilt es zu fördern. Die abstrakten Werkzeuge sind zwar mächtig und gelegentlich auch faszinierend, im Alltag sind sie aber nicht immer von jedermann handhabbar.

Verschiedene Berechnungssituationen verschieden sein lassen

„Prozentrechnen“ bei den Köchen

Im beruflichen Alltag von Köchen und Köchinnen gibt es zwei, vielleicht drei Situationen, in denen Prozentangaben eine Rolle spielen:

• Mehrbedarf: Die benötigte Menge eines Ausgangsprodukts ermitteln.
• Mehrwertsteuer: Preise auf der Speisekarte anschreiben.
• Brotrezept: Ein Brot backen.

Mehrbedarf

Werden Karotten geschält, fällt etwas weg, d.h. die geschälten Karotten sind leichter, als es die ungeschälten waren. Wenn man nun 10 kg geschälte Karotten haben möchte, stellt sich die Frage, wie viel Kilogramm ungeschälten Karotten benötigt werden.

In professionellen Kochbüchern werden als Basis für entsprechende Berechnungen sogenannte „Verlustangaben“ in Prozent publiziert (beispielsweise Pauli, 2010). Auf mehreren Seiten findet man dort Angaben zu „Schälverlusten“, „Entkernverlusten“, „Parierverlusten“ „Garverlusten“ etc.

Beispielsweise verliert man beim Schälen und Putzen folgende Anteile

• Karotten 15 %
• Erbsen 50 %
• Kopfsalat 33 %

Die 10 kg Karotten, die nach dem Schälen übrig bleiben sollen, sind also etwa 85% der ursprünglichen Menge. Und damit man am Schluss wirklich 10 kg hat muss man folglich mit etwa 11.764 kg beginnen.

Mehrwertsteuer

Bezahlt ein Gast 18.50 Fr. für einen Tagesteller, wird dafür eine Mehrwertsteuer fällig. Diese beträgt in der Schweizer Gastronomie 8%. Diese 8% beziehen sich allerdings nicht auf den vom Gast bezahlten Betrag, sondern berechnen sich als Zuschlag zum Basisverkaufspreis.

18.50 Fr. entsprechen also 108%. Der Basisverkaufspreis ist 17.13 Fr. und die die Mehrwertsteuer beträgt 1.37 Fr.

Brotrezept

Vielleicht wird in der Küche auch einmal ein Brot gebacken und es sollen 12 kg Teig nach folgendem Rezept zubereitet werden:

• Weizenmehl 80%
• Schrot 20%
• Wasser 75%
• Hefe 4%
• Salz 2%

In professionellen Brotrezepten werden die Zutaten mit Prozentwerten angegeben. Bezugsgrösse ist die Mehlmenge; hier Weizenmehl und Schrot zusammen, die 100% entsprechen. 75% Wasser bedeutet also, dass man zu einem 1 kg Mehl 750 g Wasser zugeben muss. Der Gesamtteig kommt bei diesem Rezept auf 181%, für 12 kg Teig braucht man also 6.630 kg Mehl. Die restlichen Zutaten ergeben sich relativ zum Mehl.

(Die 12 kg Teig ergeben 10 kg Brot: 16% Backverlust!)

Natürlich könnte man nun davon ausgehen, dass in allen drei Situationen dasselbe mathematische Werkzeug „Prozentrechnung“ anwendbar ist, dass also die Lernenden nur wissen müssen, wie „Prozentsatz“, „Prozentwert“ und „Grundwert“ zusammenhängen, um mittels dieses Werkzeugs alle drei Situationen bewältigen zu können.

Aber auch dieses Werkzeug ist zu abstrakt: Einmal zeigt die Erfahrung, dass vielen Lernenden diese Abstraktionsebene mit vertretbarem Aufwand nicht zugänglich ist. Und zum zweiten kann man die jeweiligen Berechnungssituationen nur professionell bewältigen, wenn man dafür ganz konkrete Vorstellungen entwickelt, welche durch „Prozentsatz“, „Prozentwert“ und „Grundwert“ nicht abgedeckt werden. Beispielsweise ist in der Situa­tion Mehrwertsteuer der Prozentsatz ein fixer Wert, der sich nur selten und dann auch nur um wenige Prozentpunkte ändert. In der Situation Brotrezepte liegt der Wert für Wasser irgendwo zwischen 70% und 80%, andere Werte signalisieren einen Fehler. Und bei der Situation Mehrbedarf schwanken die Werte zwischen 5% und 50% und haben einen klar erkennbaren Bezug zur Beschaffenheit der zu verarbeitenden Ware.

Es ist deshalb sinnvoller, diese drei Situationen als drei unterschiedliche Situationen mit je unterschiedlichen Eigenarten zu behandeln. Jemand, der diese drei Situationen perfekt beherrscht, kann eine gute und professionelle Arbeit als Köchin oder Koch machen – auch ohne dass ihm oder ihr bewusst ist, dass „mathematisch gesehen“ die drei Situationen dieselbe Struktur haben.

Situierte Werkzeuge, Abstraktion als Bonus

Didaktisch bedeutet das, dass man am besten mit den Lernenden von der konkreten Anwendungssituation her arbeitet und mit ihnen situierte, auf die jeweilige Situation ausgerichtete Werkzeuge erarbeitet.

Beispiel Küche

Mehrbedarf: In dieser Situation ist die typische Fragestellung folgende: Ich möchte 10 kg geschälte Karotten; mit wie viel ungeschälten Karotten muss ich beginnen? Ein situiertes Werkzeug könnte hier eine Liste von „Vielfachen“ sein, von Faktoren, die angeben, wie viel mehr man benötigt. Zu diesem Zweck muss man die bekannten Verlustprozente in solche „Vielfache“ umwandeln. Bei Gurken würden dann etwa aus 5% Schälverlust, 20 % Entkernverlust und 12% Tournierverlust:

• Schälen              1.052
• Entkernen          1.250
• Tournieren         1.136

So wird auf einen Bick sichtbar, dass man, um 10 kg geschälte Gurken zu erhalten, mit 10.520 kg ungeschälter Gurken beginnen muss.

Und will man mehrere Schritte aneinander hängen, genügt es, die entsprechenden Faktoren zu multiplizieren, um einen Gesamtfaktor zu erhalten. Schälen & Entkernen & Tournieren: 1.052 x 1.250 x 1.136 = 1.493.

Mehrwertsteuer: Hier könnte die Frage sein: Wenn ich 18.50 Fr. für den Tagesteller verlange, wie gross ist dann mein Basisverkaufspreis? Abhängig davon, welche Genauigkeit benötigt wird, sind verschiedene Zugänge denkbar. Der Unterschied zwischen 8% = 0.08 und 100/108 = 0.074 ist minimal und oft dürfte es reichen, dass man für den Basisverkaufspreis trotzdem 92% des effektiven Verkaufspreises einsetzt, obwohl man weiss, dass dies nicht ganz exakt ist. Ist grössere Genauigkeit gefragt, kann man natürlich mit 92.6% rechnen. Dieser Wert muss jeweils neu berechnet werden, wenn der Mehrwertssteuersatz sich ändert, und kann dann bis zur nächsten Anpassung beibehalten werden.

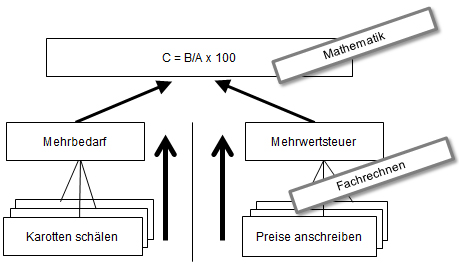
Abbildung 5: Situierte Werkzeuge und Abstraktion als Bonus in der Küche

Fühlen sich die Lernenden einmal in beiden Situationen sicher, spricht selbstverständlich nichts dagegen, mit ihnen zusammen die beiden Situationen zu vergleichen und Ähnlichkeiten herauszuarbeiten. Vorausgesetzt ist dabei, dass dafür Zeit vorhanden ist und dass sich die Lernenden für solch abstraktere Überlegungen begeistern können. V.a. für Lernende, die an eine Berufsmaturität denken oder für später höhere Weiterbildungen ins Auge fassen, dürfte ein solcher Abstraktionsversuch nützlich sein.

Etwas plakativ könnte man dabei die Auseinandersetzung mit den situierten Werkzeugen als Fachrechnen und die Diskussion über die Ähnlichkeit der Situationen als Mathematik bezeichnen.

Beispiel Milchtechnologen

Bei den Milchtechnologen kann es vorkommen, dass die vorhandene Menge Milch von Liter in Kilogramm umgerechnet werden muss, oder umgekehrt. Es lassen sich zwei Berechnungssituationen ausmachen:

• Anlieferung: Grössere Mengen Milch, welche per Tanklaster angeliefert werden, werden bei der Lieferung per Volumen erfasst. Abgerechnet wird aber in Kilogramm. Zu diesem Zweck muss die Menge gelieferte Milch von Liter in Kilogramm umgerechnet werden.
• Lagerung: Beim Zentrifugieren sind 2‘400 kg Magermilch angefallen. Diese müssen irgendwo gelagert werden und auf der Suche nach einem Tank von geeigneter Grösse muss die Menge Milch von kg in Liter umgerechnet werden.

Für die erste Situation muss man wissen, wie schwer ein Liter Milch ist. Bei Vollmilch sind das 1.030 kg. Ein nützliches Werkzeug für diese Situation wäre beispielsweise eine Tabelle der folgenden Art:

Liter	kg
1	1.030
100	103
1000	1030
.

Die Berechnungen müssen dabei recht genau erfolgen, da es darum geht, wer wie viel Geld bezahlt bzw. erhält. In der zweiten Situation muss man wissen, wie viel Platz ein Kilogramm Milch braucht. Man könnte dazu eine analoge Tabelle machen:

kg	Liter
1	0.971
100	97.1
1000	971
.

Allerdings ist hier kaum je äusserste Präzision gefragt. Geht man einfach davon aus, dass ein Kilogramm etwa einen Liter Platz braucht, ist man mit der Schätzung des benötigten Volumens auf der sicheren Seite ohne viel Platz zu verschwenden.

Der mathematische Überbau über die beiden Situationen wäre der als Formel dargestellte Zusammenhang zwischen Volumen, Masse und Dichte (d):

m = d × V

Auch hier spricht nichts dagegen, sofern Zeit und Interesse vorhanden ist, die mathematische Verwandtschaft zwischen den beiden Situationen anhand dieser Formel zu diskutieren. Nur diese Formel ist nicht Voraussetzung dafür, um kompetent mit den beiden Situationen umgehen zu können. Sie bietet lediglich eine elegante Zusammenfassung für diejenige, welche die Situationen kennen.

Wissenspakete

Gute situierte Werkzeuge stellen eine Verbindung zwischen drei verschiedenen Welten her:

• Die Welt der Dinge: In jeder beruflichen Berechnungssituation spielen konkrete Dinge wie Karotten oder Milchmengen eine Rolle. Und diese Dinge haben Eigenschaften, die man kennen und berücksichtigen muss. Beispielsweise ist es nützlich zu wissen, dass ein Milchtank mit einem Fassungsvermögen von 10‘000 Liter natürlich auch für 9‘710 Liter Platz hat.
• Die Welt der Konzepte: Die in den Berechnungssituationen vorkommenden Grössen stehen zueinander in Beziehung. Diese Beziehungen muss man kennen, um daraus Folgerungen ableiten zu können. In beruflichen Berechnungssituationen spielen dabei sehr häufig proportionale Beziehungen eine Rolle: Wenn sich diese Grösse verdoppelt (beispielsweise die Anzahl Liter Milch), dann verdoppelt sich auch jene Grösse (beispielsweise das Gewicht der Milch). Die Welt der Konzepte bietet ein mathematisches Modell für gewisse Aspekte der Welt der Dinge.
• Die Welt der Rechenverfahren: Das mathematische Modell kann man verwenden, um für konkrete Werte (beispielsweise eine bestimmte Anzahl Liter Milch) unter Nutzung der vorhandenen Beziehungen geeignete Schlussfolgerungen über andere Werte (beispielsweise das Gewicht dieser Milch) abzuleiten. Dazu benötigt man Rechenverfahren, wie etwa die Multiplikation der Milchmenge in Liter mit dem Gewicht eines einzigen Liters.

Was die Lernenden also aufbauen müssen, ist für jede Berechnungssituation ein gut integriertes Wissenspaket mit Wissen zu all diesen drei Welten. Im Falle der Situation Brotrezept könnte das beispielsweise sein (vgl. Abbildung 6):

• Dinge: Ein Brotteig setzt sich im Wesentlichen aus Mehl und Wasser zusammen. Wasser braucht es dabei etwas weniger als Mehl. Mehl wird typischerweise auf der Waage gewogen. Wasser wird typischerweise mit einem Gefäss abgemessen, wobei ein Liter praktisch einem Kilogramm entspricht. Dazu gibt es noch weitere Zutaten, die aber in wesentlich kleineren Mengen als Mehl oder Wasser in den Teig eingehen.
• Konzepte: Die Menge jeder einzelnen Zutat wird relativ zu einer Referenzmenge angegeben.
• Rechenverfahren: Die benötigte Menge einer Zutat erhält man, indem man die Referenzmenge durch 100 teilt und mit dem Anteil (in Prozent) der Zutat multipliziert.

Abbildung 6: Wissenspaket beim Arbeiten mit professionellen Brotrezepten

• Zusammenhänge: Als Referenzmenge dient die Mehlmenge. Entsprechend beträgt der Anteil des Mehls 100%. Der Anteil des Wassers liegt typischerweise zwischen 70% und 80%. Der Anteil der restlichen Zutaten liegen typischerweise unter 5%.

Ein solches Wissenspaket entsteht nicht von selbst. Es setzt erst einmal ausreichend Erfahrungen mit der realen Berechnungssituation voraus. Aus diesen Erfahrungen gibt sich Wissen über die betroffenen „Dinge“ und ihre Eigenschaften, Wissen über Abläufe und die sich daraus ergebenden Fragen, Wissen über die situationsangemessene Genauigkeit beim Berechnen etc. Es macht wenig Sinn im Unterricht Berechnungssituationen zu behandeln, zu denen den Lernenden diese Erfahrungen fehlen.

Zum Zweiten ist wichtig, dass sich die Lernenden über die Zusammenhänge zwischen den in der Berechnungssituation relevanten Grössen bewusst sind. Wenn ich diese Grösse verändere, welche anderen Grössen verändern sich dann wie? Meist sind diese Zusammenhänge nicht sehr komplex. Ein sicheres Arbeiten in den der jeweiligen Berechnungssituation ist aber nur möglich, wenn sie durchschaut werden. Dies erreicht man am besten über eine spielerische Auseinandersetzung mit was-wäre-wenn Fragen.

Und drittens stellt sich Routine im Umgang mit der Berechnungssituation und der Ableitung konkreter Resultate für konkrete Gegebenheiten nur über Übung ein. Übung braucht Zeit. Es ist deshalb sinnvoll, die im Unterricht zur Verfügung stehende Zeit gut zu nutzen und sich auf die Fragestellungen zu beschränken, welche im Berufsalltag in der entsprechenden Berechnungssituation tatsächlich vorkommen.

Horizontaler Transfer

Im Extremfall erwerben die Lernenden das notwendige Wissenspaket für jedes neue situierte Werkzeug von Grund auf neu. So ist es denkbar dass Köchinnen und Köche wenn sie nach der Situation „Mehrbedarf“ zur Situation „Mehrwertsteuer“ gehen dort wieder frisch beginnen, als hätten sie noch nie etwas von „Prozenten“ gehört.

Manchmal mag das sogar der sinnvollste Weg sein, da jeder Versuch, die Ähnlichkeit zwischen den beiden Situationen zu betonen, mehr verwirrt als dass er hilfreich wäre. Allerdings hängt dies davon ab, wie abstrakt die Gebilde sind, die man wählt, um die Ähnlichkeit zu beschreiben. Manchmal ist es möglich, mit Hilfe einer situierten, relativ konkreten Abstraktion zu arbeiten, die es den Lernenden ermöglicht einen horizontalen Transfer von einer unvertrauten zu einer vertrauten Situation zu machen.

Zitierte Literatur

• Gerster, H.-D., & Schultz, R. (2004). Schwierigkeiten beim Erwerb mathematischer Konzepte im Anfangsunterricht. Bericht zum Forschungsprojekt „Rechenschwäche – Erkennen, Beheben, Vorbeugen“. Freiburg i.Br.: Pädagogische Hochschule Freiburg, Institut für Mathematik und Informatik und ihre Didaktiken.
• Heymann, H. W. (1996). Allgemeinbildung und Mathematik. Weinheim: Beltz.
• Hoyles, C., Noss, R., & Pozzi, S. (2001). Proportional Reasoning in Nursing Practice. Journal for Research in Mathematics Education, 32(1), 4-27.
• Pauli, P. (2010). Lehrbuch der Küche. Neuhausen a.R.: Pauli Fachbuchverlag.
• van der Kooij, H. (2001, Mai). Mathematics and Key Skills for the Workplace. ALM Newsletter.
• Vergnaud, G. (1990). Epistemology and Psychology of Mathematics Education. In P. Nesher & J. Kilpatrick (Eds.), Mathematics and Cognition. A Research Synthesis by the International Group for the Psychology of Mathematics Education (pp. 14-80). Cambridge MA.: Cambridge University Press.