pdf   Bereits 1985 schreiben Dennerlein, Manthey, & Pörksen im Buch Mathematik in der Berufsschule. Analysen und Vorschläge zum Fachrechenunterricht:

„Einen Nivellierungskurs in Sachen Grundrechenarten lehnen wir ab. Wir plädieren für eine Integration dieser Gebiete in die anderen Lernabschnitte. Nach unseren Erfahrungen bleibt der Erfolg eines solchen Lernabschnitts in der Regel bescheiden. Weiter sind wir der Auffassung, dass der mathematische Unterricht in der Berufsschule nicht mit dem Aufholen tatsächlicher oder vermeintlicher Versäumnisse des Unterrichts der Sekundarstufe I beginnen sollte. Schließlich meinen wir, dass man den Schülern, die oft negative Mathematikerfahrungen mitbringen, in einem neuen Bildungsabschnitt eine neue Chance durch einen neuen Unterrichtsstoff geben sollte.“ (S. 90)

Trotz dieser klaren Stellungnahme aus dem Jahr 1985 ist es an vielen Berufsfachschulen nach wie vor üblich, alle neu eintretenden Lernenden einem Mathematik- bzw. Rechentest zu unterziehen. Diejenigen, die dabei ungenügend abschneiden, werden dann einem „Förderkurs“, einer Einheit „Nachholbildung“ oder ähnlichen Gefässen zugewiesen. Ziel dieser Massnahme ist es, „tatsächliche oder vermeintliche Versäumnisse des Unterrichts der Sekundarstufe I“ (Dennerlein et al.; siehe oben) aufzuarbeiten.

Es gibt verschiedene Gründe, warum dies nicht funktionieren kann.

Testqualität

Alle Lernenden zu testen ist nur nützlich, wenn die Lernenden korrekt klassifiziert werden, d.h. wenn genau die Lernenden in einen Kurs geschickt werden, die dort auch hingehören. Wie gut Tests sein müssen, um diesen Anforderungen zu genügen, lässt sich anhand von Abbildung 1 illustrieren.

Das Beispiel geht davon aus, dass dieses Jahr 1000 Lernende neu eintreten und getestet werden sollen. Wenn aus langjährigen sorgfältigen Beobachtungen bekannt ist, dass etwa 10% aller Lernenden über ungenügende Kompetenzen verfügen, dann ist zu erwarten, dass  in diesem Jahr etwa 100 über ungenügende Kompetenzen verfügen werden.

Da nicht bekannt ist, wer von den Lernenden dazu gehört, werden alle getestet. Nehmen wir an, dass ebenfalls aus langjährigen Beobachtungen bekannt ist, dass von denen, die über ungenügende Kompetenzen verfügen, 30% den Eintrittstest trotzdem bestehen (beispielsweise weil sie die eine oder andere Aufgabe zufälligerweise schon kannten oder weil sie zufälligerweise die richtige Antwort angekreuzt haben etc.). Dann ist zu erwarten, dass von den 100 schwachen Lernenden etwa 70 dem Stützkurs zugewiesen werden und etwa 30 der schwachen Lernenden unentdeckt bleiben.

Nehmen wir weiterhin an, dass typischerweise von den Lernenden mit genügend Kompetenzen 40% den Test trotzdem nicht bestehen, weil sie beispielsweise am Tag vorher sehr spät zu Bett gegangen sind oder weil sie gerade in einer kleineren oder grösseren Lebenskrise stecken etc. Dann ist zu erwarten, dass von den 900 Lernenden mit genügenden Kompetenzen etwa 360 fälschlicherweise dem Kurs zugewiesen werden. Alles in allem werde so Kursplätze für 430 Lernende (70 + 360) benötigt. Von diesen 430 Lernenden sitzen aber 360, also etwa 84%, fälschlicherweise im Kurs.

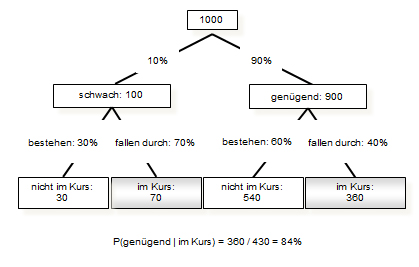
Abbildung 1: Prozentsatz Lernender, die fälschlicherweise im Kurs sitzen – ein Beispiel

Selbstverständlich kann man gegenüber dem Beispiel in Abbildung 1 einwenden, dass es sich offenbar um einen nicht besonders guten Test handelt: 40% der Lernenden mit genügenden Kompetenzen fallen durch! Wenn Sie gerne mit Zahlen spielen, können Sie an dieser Stelle selbst überprüfen, was sich ändert,  wenn Sie an Stelle der 30% Schwachen, die fälschlicherweise bestehen, und der 40% Genügenden, die fälschlicherweise durchfallen, andere Werte einsetzen.

Wenn man beginnt, den Test zu „verbessern“ – also beispielsweise annimmt, dass nur 10% der Lernenden mit genügenden Kompetenzen den Test nicht bestehen – wird man aber bald feststellen, dass es schwierig ist, die Situation wirklich zu verbessern. Strebt man beispielsweise an, dass höchstens noch 5% der Lernenden im Kurs fälschlicherweise dort sind, wird man feststellen, dass man die Spezifität des Tests (Wie viele Lernende mit genügender Kompetenz bestehen den Test?) auf absurde 99,5% anheben muss. Ein Wert, der in Realität sicher nicht erreichbar ist.

Schaut man sich die Zahlen im Beispiel an, wird deutlich, dass das Problem dadurch entsteht, dass die Gruppe der Lernenden mit genügender Kompetenz so gross ist: 900 Lernende. Auch wenn nur ein kleiner Prozentsatz davon durch den Test falsch eingeteilt wird, sind das absolut gesehen schnell viele Personen. Aber auch wenn man diese Gruppe verkleinert, also beispielsweise annimmt, dass nur 75% der Lernenden genügend Kompetenzen aufweisen, muss die Spezifität des Test immer noch 98% erreichen – wie Sie leicht selbst überprüfen können!

Die realen Zahlen sind für keine Berufsfachschule bekannt, die Eintrittstests durchführt. Weder ist bekannt, wie gross der Prozentsatz der schwachen Lernenden wirklich ist, noch ist bekannt, wie gross die Spezifität der eingesetzten Tests ist. Und es wäre auch nicht ganz einfach, diese Zahlen zu erheben. Aber unabhängig davon zeigen die Rechenbeispiele, dass die Anforderungen an einen wirklich nützlichen Test so hoch sind, dass sie auch durch eine sorgfältige Testentwicklung nicht zu erreichen wären.

Elisabeth Moser Opitz hat über einige Jahre hinweg einen professionellen, wissenschaftlich abgesicherten Test namens BASIS-MATH entwickelt und Daten dazu publiziert (Moser Opitz & Ramseier, 2012). Der Test soll helfen, Kinder mit Rechenschwäche zu diagnostizieren. Wie alle Testentwicklerinnen hat Moser Opitz das Problem, dass es keine Möglichkeit gibt, „direkt“ herauszufinden, welche Kinder wirklich rechenschwach sind. Um ein Kind als rechenschwach zu diagnostizieren braucht es immer einen Test bzw. das Urteil einer Lehrperson oder anderer Spezialisten. Moser Opitz vergleicht deshalb unter anderem die Einteilung in rechenschwach/nicht rechenschwach durch den Test mit dem Urteil der Lehrenden der Kinder (Tabelle 1).

Tabelle 1: Häufigkeiten rechenschwacher Kinder im Urteil von BASIS-MATH bzw. von Lehrpersonen (nach Tabelle 7 in Moser Opitz & Ramseier, 2012)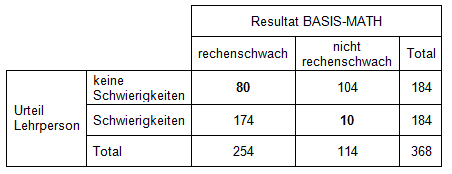

Die Resultate zeigen, dass 80 von 254 Kindern, welche der Test als rechenschwach einstuft, nach Meinung der Lehrpersonen keine Schwierigkeiten mit dem Rechen haben, also ganze 31%. D.h. ganze 31% der Kinder, die auf Grund des Tests speziell gefördert werden sollten, können laut dem Urteil der Lehrenden offenbar dem Unterricht folgen und fallen nicht weiter auf. Auch wenn es hier um einen wissenschaftlich abgestützten Test für Kinder der vierten bis achten Klasse geht und ein direkter Schluss auf schuleigene Eintrittstest nicht direkt möglich ist, zeigen die Zahlen doch, dass eine Spezifität von über 90% realistischerweise nicht zu erreichen ist. Es ist also unwahrscheinlich, dass es irgendwo einen Test gibt oder je geben wird, der verlässlich genug zwischen Lernenden mit und ohne ausreichende Rechenkompetenzen unterscheiden kann. Und absolut sicher ist, dass sich ein solcher Test nicht mit den schulintern vorhandenen Mitteln entwickeln lässt.

Kontextgebundenheit von Wissen und Können

Ein Grund dafür ist der, dass viele Menschen nicht unabhängig von der konkreten Anwendungssituation „Prozentrechnen“ etc. können und es auch nie lernen werden (vgl. Wissensaufbau von den Füssen her). Wenn sie „Prozentrechnen“ können, dann immer in bestimmten Kontexten, wie beispielsweise „Rabatte beim Einkaufen“ oder „Zuckeranteil in Frühstücksflocken“. Die Aufgaben eines Eintrittstests treffen nun entweder einen Kontext, welcher den Lernenden vertraut ist, oder sie verfehlen ihn. In beiden Fällen kann es zu einer Fehleinschätzung kommen.

Treffen die Aufgaben den Kontext, dann werden die Lernenden die Aufgabe lösen können, d.h. sie erhalten das Etikett „kann Prozentrechnen“. Es ist aber durchaus denkbar, dass es ihnen nicht gelingt, später aus diesem vertrauten Kontext in den neuen beruflichen Kontext einen Transfer zu machen und dass sie folglich im Unterricht nicht „Prozentrechnen“ können.

Treffen umgekehrt die Aufgaben den Kontext nicht, dann werden die die Lernenden die Aufgabe nicht lösen können, werden also der Gruppe „kann nicht Prozentrechnen“ zugewiesen. Und hier es ist umgekehrt denkbar, dass sie später im Unterricht sehr wohl einen Transfer aus einem vertrauten Kontext in den geforderten beruflichen Kontext machen können, dass sie also im Unterricht überraschenderweise „Prozentrechnen“ können.

Versucht man im Test verschiedene Kontexte anzusprechen, dann erhält man typischerweise gemischte Resultate die schwierig zu interpretieren sind – einige Aufgaben werden gelöst, andere nicht. Abbildung 2 enthält zwei Aufgaben aus einem solchen Eintrittstest. Die erste Aufgabe wird von den Lernenden typischerweise ohne grosse Probleme gelöst, bei der zweiten haben sie hingegen Schwierigkeiten. Dies übrigens, obwohl die zweite Aufgabe bewusst einen zukünftigen beruflichen Kontext vorwegnimmt, der aber eben noch nicht vertraut ist.

Anwendung: Kaufen

Eine Sportjacke kostet normalerweise CHF 150.-. Nun wird sie mit einem Rabatt von 30% billiger verkauft. Wie teuer ist die Sportjacke jetzt?

 

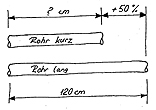
Anwendung: Fachrechnen

Ein Metallrohr ist 120 cm lang. Es ist um 50% länger als ein kürzeres Rohr. wie lang ist das kürzere Rohr?

Abbildung 2: Zwei angewandte Aufgaben aus einem Eintrittstest

 (Selbstverständlich kann man auch argumentieren, dass die grössere Schwierigkeit der zweiten Aufgabe daher rührt, dass im Gegensatz zur ersten Aufgabe der Grundwert gesucht wird und dass Prozentsätze über 100% vorkommen. Dies lässt sich nicht wegdiskutieren. Dass aber Prozentsätze über 100% überhaupt Schwierigkeiten machen, hat seinerseits wieder damit zu tun, dass dies in typischen vertrauten Kontexten wie Rabatte etc. nicht vorkommt, dass dort 100% als „Ganzes“ immer die obere Grenze ist.)

Statisches Bild

Die Entwicklung eines nützlichen Tests zu mathematischen Kompetenzen sieht sich also mit einigen Schwierigkeiten konfrontiert. Aber sogar wenn es gelingen würde, Test zu entwickeln, welche zuverlässig das relevante situierte Wissen erfassen können, ist fraglich, ob diese wirklich nützlich wären. Denn genau genommen interessiert nicht, was die Lernenden im Moment des Eintrittstests wissen. Entscheidend für ihren Erfolg an der Berufsfachschule ist viel mehr, ob sie anschliessend dem dort stattfindenden Unterricht folgen können. Zwischen diesen beiden Dingen besteht nicht notwendigerweise ein direkter Zusammenhang.

Es sind verschiedene Gründe dafür vorstellbar. Einmal ist es durchaus möglich, dass Lernenden, die beispielsweise sehr wohl in verschiedenen Kontexten „Prozentrechnen“ können, auf eine Lehrperson treffen, die das für den entsprechende Beruf relevante „Prozentrechnen“ so darstellt, dass die Lernenden die Ähnlichkeit zwischen den ihnen vertrauten Kontexten und dem neuen Kontext nicht erkennen können. Das kann daran liegen, dass die Lehrperson nicht darin geschult ist, das mathematische Vorwissen der Lernenden aufzugreifen. Es kann aber auch sonst geschehen. Manchmal gibt es einfach Unverträglichkeiten zwischen dem Denken gewisser Lernenden und ihren Lehrpersonen.

Der umgekehrt Fall ist aber auch vorstellbar. Das in einen beruflichen Kontext eingebettete „Prozentrechnen“ ist typischerweise nicht besonders anforderungsreich. Es ist durchaus denkbar, dass Lernende, die in ihrer bisherigen Schulkarriere aus irgend welchen Gründen in keinem einzigen Kontext „Prozentrechnen“ gelernt haben, im neuen beruflichen Kontext sehen, wozu die entsprechenden Berechnungen gebraucht werden, und so in kürzester Zeit für diesen Kontext „Prozentrechnen“ lernen. Diese Möglichkeit haben Dennerlein et al. vor Augen, wenn sie im eingangs erwähnten Artikel fordern, „dass man den Schülern, die oft negative Mathematikerfahrungen mitbringen, in einem neuen Bildungsabschnitt eine neue Chance durch einen neuen Unterrichtsstoff geben sollte.“

Ein sinnvoller Eintrittstest müsste deshalb nicht überprüfen, was die Lernenden im Moment des Eintritts können, sondern ob sie in der Lage sind, genügend schnell dazuzulernen. Solche Lerntests sind möglich. Beispielsweise war es früher in einer Schule für Dentalhygiene üblich, einen solchen Eintrittstest bezüglich manuellen Fertigkeiten zu machen. Personen, die sich für die Ausbildung interessierten, erhielten eine kleine, mit Nagellack überzogene Kugel und ihnen wurde gezeigt, wie man mit Hilfe eines dentalhygienischen Instruments diesen Nagellack systematisch entfernen kann. Sie erhielten dann eine Woche Zeit, dieses Vorgehen zuhause zu üben. Anschliessend wurde überprüft, wie grosse Fortschritte sie dabei gemacht hatten. Zur Ausbildung zugelassen wurden diejenigen, deren Fortschritte gewisse minimale Anforderungen erfüllten.

Unterricht als „Lerntest“

Es wäre eine spannende Herausforderung einen entsprechenden Lerntest für „Prozentrechnen“ etc. zu entwickeln. Allerdings wäre der Aufwand sehr gross (denn beispielsweise müsste er ja kontinuierlich an die Lehrstile der entsprechenden Lehrenden angepasst werden) und der Ausgang ungewiss (man denke an die Zahlen im Abschnitt „Testqualität“ oben). Glücklicherweise ist es aber absolut unnötig, diesen Aufwand auf sich zu nehmen. Ein entsprechender, äusserst verlässlicher „Lerntest“ existiert bereits: Man schickt die Lernenden ein paar Wochen in den Regelunterricht und beobachtet, ob sie diesem folgen können. Ist dies der Fall, sind keine weiteren Massnahmen notwendig. Haben sie hingegen Schwierigkeiten, benötigen sie zusätzliche Unterstützung!

Ein Eintrittstest dieser Art hat verschiedene Vorteile:

• Er ist absolut zuverlässig: Haben Lernende Schwierigkeiten, dem Regelunterricht zu folgen, dann kann man sicher sein, dass sie Schwierigkeiten haben, dem Regelunterricht zu folgen.
• Er ist multidimensional: Es werden keine einschränkenden Annahmen darüber getroffen, was alles Ursachen für solche Schwierigkeiten sein könnten. Der Test reagiert auf jede beliebige Ursache.
• Er ist billig: Es ist keine Testentwicklung notwendig. Ãœberwachen, ob die Lernenden im Unterricht lernen, was sie lernen sollten, gehört zu den normalen Aufgaben jeder Lehrperson.
• Er verunsichert nicht unnötig: Lernende mit einer negativen Schulkarriere erhalten eine Chance in einem neuen Umfeld unbelastet einen Neuanfang zu machen.

Damit dieser Test funktioniert, müssen allerdings zwei Voraussetzungen gegeben sein:

• Die Lehrpersonen müssen in den ersten drei, vier Monaten der Ausbildung kontinuierlich überprüfen, ob Lernende Schwierigkeiten haben, dem Unterricht zu folgen, und mit entsprechenden Lernende sobald als möglich das Gespräch suchen – etwa im Sinn von: „Mein Eindruck ist, dass Sie Mühe haben, dem Unterricht zu folgen. Wir haben da ein Stützangebot, das Ihnen helfen könnte. Was meinen Sie, wäre das etwas für Sie?“
• Die Diagnose, mit der die Lernenden in den Stützunterricht kommen, lautet „Kann meinem Unterricht nicht folgen.“ Woran das liegt, ist in diesem Moment noch nicht geklärt. Der Stützunterricht muss deshalb so organisiert sein, dass es möglich ist, flexibel auf die jeweiligen Schwierigkeiten der Lernenden einzugehen.

Zitierte Literatur

• Dennerlein, J., Manthey, H. B., & Pörksen, S. H. (1985). Ãœberlegungen zu einer Neuorientierung des mathematischen Unterrichts in der Teilzeit-Berufsschule im Berufsfeld Wirtschaft und Verwaltung. In P. Bardy, W. Blum & H.-G. Braun (Eds.), Mathematik in der Berufsschule. Analysen und Vorschläge zum Fachrechenunterricht (pp. 72-91). Essen: Girardet.
• Moser Opitz, E., & Ramseier, E. (2012). Rechenschwach oder nicht rechenschwach? Eine kritische Auseinandersetzung mit Diagnosekonzepten, Klassifikationssystemen und Diagnoseinstrumenten unter besonderer Berücksichtigung von älteren Schülerinnen und Schülern. Lernen und Lernstörungen, 1(2), 99-117.