pdf Viele Berufsfachschulen machen einen Eintrittstest im Bereich Rechnen/Mathematik und empfehlen dann Lernende, welche in diesem Test ungenügende Resultate ausweisen, einem Förderkurs zu besuchen. Die Logik hinter diesem Vorgehen ist die folgende (vgl. Abbildung 1):

• Damit die Lernenden dem Unterricht folgen können, müssen sie über bestimmte Kompetenzen verfügen.
• Ob sie über diese Kompetenzen verfügen, wird mittels eines Tests festgestellt.
• Lernende, bei denen sich dabei zeigt, dass sie nicht über die benötigten Kompetenzen verfügen, erhalten die Gelegenheit, diese in einem speziellen Förderkurs aufzubauen.
• Sobald sie dann über die benötigten Kompetenzen verfügen, können sie vom normalen Unterricht profitieren. 

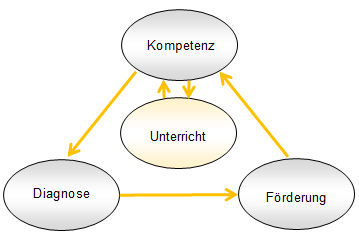
Abbildung 1: Das Dreieck von Unterricht/Kompetenzmodell, Diagnose und Förderung

Entscheidend bei dieser Überlegung ist der Ausgangspunkt im ersten Satz: „Damit die Lernenden dem Unterricht folgen können …“. D.h. welche Kompetenzen gefordert sind und folglich welche Art der Diagnose und welche Art der Förderung benötigt wird, hängt direkt vom Unterricht, vom im Unterricht gewählten didaktischen Modell ab.

Das „klassische“ Modell

Eine didaktische Variante ist der Weg „von oben nach unten“ (vertikaler Transfer, vgl. Horizontaler Transfer). Im Unterricht wird vorausgesetzt, dass die Lernenden kontextunabhängig beispielsweise „Prozentrechnen“ können. Sie wissen Bescheid über Grundwert, Prozentwert und Prozentsatz und deren Zusammenhänge und können dieses Wissen nach Bedarf einsetzen. Der Unterricht selbst besteht dann darin, die neue Berechnungssituation – beispielsweise Verlustrechnungen in der Küche – einzuführen und dann die Lernenden ihr Wissen auf diese Situation anwenden zu lassen.

Vorausgesetzt wird also eine kontextunabhängige Rechenkompetenz wie „Prozentrechnen können“ (vgl. Abbildung 2). Konsequenterweise überprüft man das Vorhandensein dieser Kompetenz mit einer Auswahl möglichst unterschiedlicher Aufgaben, die breit über verschiedene Kontexte streuen. Ein typisches Beispiel dafür ist folgende Aufgabe aus einem älteren Lehrmittel für Köche: „Eine Garageneinfahrt ist 12,5 m von der Strasse entfernt und 4 m vertieft geplant. Wie viel Gefälle in Prozent wird sie aufweisen?“

Sollte sich dabei zeigen, dass einzelne Lernende mehrere dieser Aufgaben nicht lösen können, dann können sie offensichtlich nicht kontextfrei Prozentrechnen, d.h. die für den Unterricht notwendigen Voraussetzungen sind nicht gegeben. Konsequenterweise werden diese Lernenden einem Förderkurs für „Prozentrechnen“ zugewiesen, wo sie die Gelegenheit erhalten, die Kompetenz „kontextfrei Prozentrechnen können“ aufzubauen. Ist dieser Förderkurs erfolgreich, sind damit die Voraussetzungen für den vorgesehen didaktischen Ablauf des Regelunterrichts gegeben und der Regelunterricht kann wie vorgesehen stattfinden.

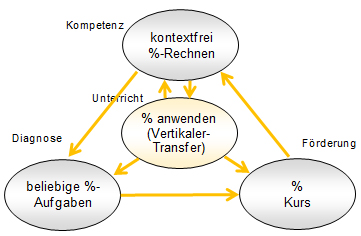
Abbildung 2: Das klassische Dreieck mit der problematischen Annahme, dass es „kontextfreie Rechenkompetenz“ gibt

Vom Kopf auf die Füsse gestellt

Das Problematische am „klassischen“ Modell ist die Annahme, dass es so etwas wie kontextfreie Kompetenzen, also beispielsweise kontextfreies „Prozentrechnen“ gibt (vgl. Wissensaufbau von den Füssen her). Gibt es solche Kompetenzen nicht, dann bricht das ganze oben geschilderte „klassische“ Modell in sich zusammen und muss durch ein anderes ersetzt werden. Oder, wie Grassi et al. (2014) unter dem Titel „Das Problem der fehlenden Kontextualisierung“ schreiben: „Standortbestimmungen im Bereich Mathematik/berufliches Rechnen sind also mit der nötigen Vorsicht anzugehen …“ (S. 54).

Ein alternatives, hier vorgeschlagenes didaktisches Modell ist der horizontale Transfer. Dieser geht nicht von einer kontextfreien Kompetenz aus, sondern baut darauf auf, dass die Lernenden zumindest eine Ausgangssituation beherrschen, aus der sich Wissen und Können auf eine Zielsituation übertragen lassen. Beispielsweise könnte das für das Verlustrechnen in der Küche bedeuten, dass der Unterricht beim Gebrauch von Prozentangaben in der Situation „Rabatte beim Einkaufen“ anknüpft und den Lernenden hilft, zu sehen, in welchen Punkten die Zielsituation „Verluste beim Kochen“ dieser Ausgangssituation ähnlich ist.

Vorausgesetzt wird hier also, dass die Lernenden alle über mindestens eine kontextualisierte Kompetenz verfügen, die sich für einen horizontalen Transfer in die Zielsituation eignet, also beispielsweise mit Rabatten in Prozent beim Einkaufen umgehen können (vgl. Abbildung 3).

Bei der Diagnose geht es in diesem Fall dann konsequenterweise darum zu überprüfen, ob diese Voraussetzung gegeben ist. Man wird also beispielsweise überprüfen, ob die Lernenden mit Rabatten beim Einkaufen umgehen können, indem man entsprechende Aufgaben stellt. Sofern es mehrere Situationen gibt, die als Ausgangssituation in Frage kommen (wie beispielsweise „Zuckeranteil in Nahrungsmitteln“, „Zinsen beim Sparkonto“ etc.) wird man sinnvollerweise eine Situation wählen, von der man aus Erfahrung weis, dass die meisten Lernenden damit umgehen können. Es wäre auch denkbar, mehrere dieser möglichen Situationen zu testen und dann für den Unterricht diejenige auszuwählen, bei der sich die meisten Lernenden sicher fühlen.

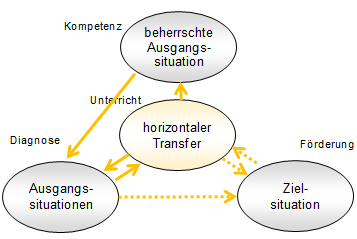
Abbildung 3: Das Dreieck zum horizontalen Transfer

Auch hier kann es sein, dass einige Lernende nicht genügende Erfahrungen mit einer möglichen Ausgangssituation mitbringen, auch wenn zu erwarten ist, dass dies deutlich weniger sind, als wenn man nach einer kontextfreien Rechenkompetenz sucht. Diese Lernenden sollten auch in diesem Fall einem Förderkurs zugewiesen werden. Nur macht es hier wenig Sinn, in diesem Kurs an den Voraussetzungen für den Regelunterricht, d.h. an der Ausgangssituation zu arbeiten. Das Ziel ist ja beispielsweise nicht, dass die Lernenden mit Rabatten beim Einkaufen umgehen können, sondern dass sie Verluste beim Kochen im Griff haben. Konsequenterweise kann man im Förderkurs direkt an dieser Zielsituation arbeiten – genauso wie beispielsweise Katy Rhiner mit Anna direkt an der Höhe des Vorhangs arbeitet (Grassi et al., 2014, S. 140ff).

Eintrittstest

Grundsätzlich könnte man auch dann, wenn der Unterricht nicht auf vertikalen, sondern auf horizontalen Transfer aufbaut, das Vorhandensein der gewünschten Voraussetzungen durch einen Eintrittstest überprüfen. Beispielsweise würde man dann anstelle beliebiger, weit streuender Prozentaufgaben eben nur Aufgaben zu einer oder einigen wenigen Ausgangsituationen stellen, mit denen man wirklich arbeiten will.

Wie beschrieben, sind solche flächendeckende Eintrittsteset aber unter anderem darum problematisch, weil die notwendige Testqualität (Spezifität) praktisch nicht erreichbar ist. Dieses Problem lässt sich nicht entschärfen, indem man von Tests auf kontextfreie Kompetenzen zu Tests auf kontextualisierte Kompetenzen übergeht. Im Gegenteil, es verschärft sich dadurch diese Problematik sogar noch. Denn es ist anzunehmen, dass Lernende, welche über eine geeignete kontextualisierte Kompetenz verfügen, häufiger anzutreffen sind, als Lernende, die „kontextfrei“ (was auch immer das heisst) rechnen können. Dadurch steigen die Anforderungen an die Spezifizität eines Tests noch weiter (vgl. Abbildung 1 in Eintrittstests), d.h. es wird nicht einfacher, sondern schwieriger, einen qualitativ guten Test zu erstellen.

Es dürfte also auch so – wie bei Eintrittstests vorgeschlagen – am sinnvollsten sein, einfach einmal mit allen Lernenden im Regelunterricht einen horizontalen Transfer, ausgehend von einer vermutlich bekannten Situation, zu versuchen und erst dann jene Lernenden, welche dabei nicht folgen können, gesondert zu behandeln.

Zitierte Literatur

Grassi, A., Rhiner, K., Kammermann, M. & Balzer, L. (2014). Gemeinsam zum Erfolg. Früherfassung und Förderung in der beruflichen Grundbildung durch gelebte Lernortkooperation. Bern: hep