pdf Dieser Text beleuchtet anhand von Forschungsresultaten die Schritte 3 bis 5 der Acht Schritte etwas genauer. Diese drei Schritte bilden eine Einheit:

1. Warten, bis die Lernenden schon Erfahrungen gemacht haben
2. Die Lernenden schildern ihre Erfahrungen
3. Mittelschwere Aufgabe stellen und die Lernenden in Gruppen erarbeiten lassen, wie sie diese mit ihrem bereits vorhandenen Wissen angehen würden.
4. Gruppenlösungen kritisch besprechen. Brauchbare Ansätze wertschätzen.
5. Werkzeuge einführen, Benutzung an realistischem Beispiel modellhaft vormachen.
6. Die Lernenden üben mit selbst erfunden Beispielen
7. Die Lernenden erarbeiten einen Spickzettel
8. Gemeinsam die Anwendung im Betrieb diskutieren

Die damit verbundene didaktische Grundidee wurde von verschiedenen Autoren unabhängig entwickelt und auch unterschiedlich benannt; beispielsweise:

Vom Singulären zum Regulären: Gallin & Ruf (1990) beschreiben damit den Lernprozess, der von den individuellen (singulären) Vorstellungen ausgeht, welche die Lernenden mitbringen, und dann die Lernenden zu einem professionellen (regulären) Verständnis führen soll.

Produktives Scheitern (productive failure): Kapur & Bielaczyc (2012) andererseits betonen, dass es im Schritt 3 nicht darum geht, dass die Lernenden die Aufgaben perfekt lösen, sondern dass gerade wenn sie (teilweise) scheitern, sich das produktiv auf den restlichen Lernprozess auswirken kann.

Funktioniert es denn?

Traditioneller Unterricht beginnt direkt mit Schritt 5. Auf diesem Hintergrund kann man sich fragen, ob die zwei zusätzlichen Schritte 3 und 4 den Aufwand wert sind. Kapur & Bielaczyc (2012) haben das in einer sorgfältigen Studie untersucht. Sie haben zwei Arten von Unterricht verglichen:

• Produktives Scheitern (PS): Die Schritte 3 bis 5 oben (Details siehe Abschnitt 3 unten)
• Direkte Instruktion (DI): Schritt 5 mit anschliessendem Ãœben (Lehrperson macht eine Einführung; Lehrperson rechnet einige Beispiele vor; Lernende lösen einige Ãœbungsbeispiele; Lehrperson diskutiert die Lösungen mit der Klasse; Lernende lösen weitere Ãœbungsaufgaben als Hausaufgaben)

Unter beiden Bedingungen dauerte der Unterricht gleich lang, d.h. etwa so viel Zeit, wie die PS Klassen für die Schritte 3 und 4 brauchten, hatten die DI Klassen Zeit für das Üben.

Verglichen wurden in drei Schulen je eine (oder zwei) PS und je eine DI Klasse im 7. Schuljahr. Die drei Schulen wurden nach dem Notendurchschnitte der Lernenden in Mathematik beim Übertrittstest nach dem 6. Schuljahr ausgewählt:

• Schule A: 5.5 (umgerechnet auf Schweizer Notenskala)
• Schule B: 4.5
• Schule C: 4.0

Alle Klassen wurden vorher und nachher mit denselben Aufgaben getestet. Vor den Unterrichtseinheiten liesst sich kein Unterschied zwischen den PS und DI feststellen. Nachher hingegen schon, wie Tabelle 1 zeigt.

Tabelle 1: Leistungen im Nachtest (Prozentsatz richtig gelöster Aufgaben)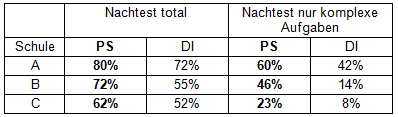

Da alle Klassen mit demselben Test getestet wurden, hatten die schwächeren Lernenden der Schule B und vor allem C mehr Mühe mit diesem Nachtest. Aber in allen Schulen schnitten die PS Klassen klar besser ab, als die DI Klassen – und das, obwohl die PS Klassen keine Übungsphase und keine Hausaufgaben hatten, und obwohl die DI Klassen im Schnitt 92% der Hausaufgaben richtig gelöst hatten!

Der Unterschied war bei Aufgaben, welche die Autoren als „typische Schulbuchaufgaben“ bezeichnen, nicht besonders gross. Aufgaben dieser Art wurden auch in der Übungsphase der DI Klassen eingesetzt. Im Test eingeschlossen waren aber auch 7 „komplexe“ Aufgaben, die sich nicht einfach direkt durch die Anwendung eines eingeübten Schemas lösen liessen, sondern bei denen etwas Nachdenken gefragt war. Hier sind die Unterschiede zwischen den DI und PS Klassen gewaltig. Gerade bei den schwächeren Klassen lösten die PS Lernenden fast drei Mal so viele Aufgaben wie die DI Lernenden!

Zusammenfassend lässt sich also festhalten:

• Es funktioniert.
• Es braucht nicht mehr Zeit. Die Zeit, welche für die Schritte 3 und 4 eingesetzt wird, kann beim Ãœben mehr als kompensiert werden.
• Auch schwächere Lernende profitieren. Vor allem wenn es um Aufgaben geht, bei denen etwas Nachdenken gefordert ist, profitieren die Schwächeren sogar noch mehr als die Stärkeren.

Warum funktioniert es?

Zuerst ein paar weitere Angaben aus Kapur & Bielaczyc (2012), die helfen können, die Wirkung von Schritt 3 bis 5 zu verstehen (s. Tabelle 2).

Interessant ist einmal, dass die PS Klassen bei den Einstiegsaufgaben tatsächlich scheitern. Auch in der leistungsstärksten Schule konnten nur 16% aller Gruppen die Einstiegsaufgabe tatsächlich lösen. Und hier dürfte der erste Grund für die Wirksamkeit des Verfahrens liegen: Die Lernenden erkennen beim Herumprobieren, wo die eigentlichen Herausforderungen bei der Behandlung der Situation liegen, und sie merken, was sie bereits selbst bewältigen können und wo sie etwas dazulernen müssen. Schliesst der Input in Schritt 5 sauber an diese Vorarbeit der Lernenden an, können sie so viel besser verstehen und würdigen, warum das „reguläre“ Vorgehen genau diese Form hat.

Tabelle 2: Bearbeitung der Einstiegsaufgabe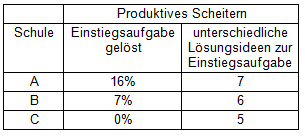

Kapur & Bielaczyc haben im Weiteren ausgewertet, wie viele verschiedene Ideen die einzelnen Gruppen produziert haben, als sie versuchten, die Einstiegsaufgabe zu lösen. Betrachte man das pro Schule, dann zeigt sich, dass auch die schwächsten Lernenden, also die aus der Schule C, viele Ideen haben (5 im Schnitt). Sie produzieren zwar etwas weniger Ideen als die stärksten Lernenden; der Unterschied ist aber nicht sehr gross. Vergleicht man pro Gruppe die Anzahl Ideen, die sie produziert haben, mit der Leistung im Nachtest, dann findet man einen klaren Zusammenhang: Je mehr Ideen eine Gruppe produzierte, umso besser sind die Leistungen nachher. Dieser Effekt ist 9-mal stärker als der Einfluss, den das Vorwissen hat (Kapur & Bielaczyc, 2012, S. 67).

Kapur & Bielaczyc sehen sich dadurch bestätigt, dass ihr Vorgehen folgende Wirkung hat:

1. Die Lernenden aktivieren relevantes Vorwissen beim Versuch, die Aufgabe zu lösen.
2. Die Lernenden entdecken, wo die kritischen Punkte bei dieser Art von Aufgaben sind – gerade weil sie die Aufgabe nicht einfach lösen können.
3. Die Lernenden setzen sich mit diesen kritischen Punkten intensiv auseinander – umso intensiver, je mehr verschiedene Lösungsideen sie ausprobieren.
4. Der darauf aufbauende Input der Lehrperson ermöglicht es ihnen, aus all diesen Erfahrungen eine brauchbare Vorstellung des „regulären“ Vorgehens zu entwickeln.
5. Der ganze Prozess führt im Weiteren dazu, dass die Lernenden das neu erworbene „reguläre“ Vorgehen zu ihrem Vorgehen machen – und nicht einfach als etwas erleben, dass sie auch noch lernen müssen, weil es auf dem Lehrplan steht.
6. Zudem setzen sich die Lernenden aktiv mit ihrem eignen Lernen und Wissen auseinander. Sie entdecken, wo sie noch zu wenig wissen, und erleben, wie sie dieses Manko beheben können.

Dem ist nicht viel beizufügen. Die Lernenden erleben auf diesem Weg das „reguläre“ Vorgehen als eine echte Antwort auf eine echte Frage. Sie kommen weg von der Schülerhaltung „Welche Antwort möchte der Lehrer wohl hören?“ und beginnen wieder zu lernen (Holt, 2004).

Dank der intensiven Vorarbeit fällt es ihnen leichter, die Erklärungen der Lehrperson zu verstehen. Sie können erkennen, was daran wirklich zentral ist, da dadurch eines ihrer Probleme beim Bearbeiten der Einstiegsaufgabe gelöst wird. Und sie können solche zentrale Aspekte besser von eher zufälligen Elementen der Erklärung der Lehrperson unterscheiden, wie etwa die Wahl des Beispiels, anhand von dem die Lehrperson das „reguläre“ Vorgehen illustriert.

Im Kontext das Fachrechens dürfte zudem auch wichtig sein, dass das neue Wissen fest mit bereits vorhandenen Erfahrungen verbunden wird. Ist die Einstiegsaufgabe eine Aufgabe/Situation, wie sie typischerweise im Betrieb vorkommt und welche die Lernenden von dort schon kennen (Schritt 1 der Acht Schritte), dann sind diese betrieblichen Erfahrungen Teil des aktivierten Vorwissens. Und die Lernenden werden anschliessend die Erklärungen der Lehrperson mit diesen Erfahrungen verbinden und auf diesem Hintergrund verstehen.

Worauf es ankommt

Wie immer gibt es verschiedenste Details zu beachten, damit das Ganze im Unterricht auch wirklich funktioniert. Hier einige Anregungen, die sich auch mit dem decken, wie die Lehrpersonen in der Studie von Kapur & Bielaczyc vorgegangen sind:

• Die Wahl der Einstiegsaufgabe: Die Einstiegsaufgabe muss die Lernenden herausfordern. Kapur & Bielaczyc halten fest, dass sie schwieriger sein muss, als das, was die Lernenden mit ihrem momentan vorhandenen Vorwissen bewältigen können. Auf der anderen Seite darf sie aber auch nicht zu schwierig sein, damit die Lernenden nicht einfach frustriert aufgeben. Geeignete anregende Aufgaben zu finden, dürfte der grösste Entwicklungsaufwand sein, den man auf sich nehmen muss, will man mit den Acht Schritten arbeiten.
  Im Kontext des Fachrechnens an Berufsfachschulen kann man das relativieren: Natürlich ist es gut, wenn die Lernenden durch die Aufgabe gefordert werden. Es macht aber keinen Sinn, künstlich „schwierige“ Aufgaben zu konstruieren. Wenn es sich beim Schritt 3 herausstellt, dass die Lernenden die Aufgabe, so wie sie sich im beruflichen Alltag typischerweise präsentiert, bereits lösen können, dann genügt das. Darüber hinaus zu gehen, macht nur Sinn, wenn Zeit und Interesse besteht.
  Es ist auch nicht zwingend, dass die meisten Gruppen zu keiner Lösung gelangen. Fruchtbar für die Diskussion in Schritt 4 ist schon, wenn die Gruppen unterschiedliche Lösungen mit unterschiedlichen Stärken und Schwächen herausarbeiten.
  Der Aufwand, gute Aufgaben zu finden, dürfte im berufsbildenden Kontext auch etwas geringer sein, als im Kontext, in dem die Untersuchung von Kapur & Bielaczyc stattgefunden hat (allgemeinbildende Schule, 7. Klasse). Echte Aufgaben aus dem beruflichen Alltag, welche die Lernenden realistischerweise am Schluss der Ausbildung beherrschen sollten, dürfen auf Lernende nicht abschreckend wirken. Denn falls die Lernenden die entsprechenden Situationen bereits im Betrieb erlebt haben (Schritt 1!), sollten sie auch motiviert sein, diese zu lösen.
• Die Arbeit an der Einstiegsaufgabe: Prinzipiell könnte man die Einstiegsaufgabe auch in Einzelarbeit bearbeiten lassen. Die Arbeit in Gruppen hat den Vorteil, dass mehr Vorwissen aktiviert wird, da mehr Köpfe beteiligten sind; und dass auch mehr unterschiedliche Lösungsideen generiert werden, was – wie die Daten zeigen – entscheidend für den Lernerfolg ist.
• Begleitung der Einstiegsaufgabe: Für die Lehrpersonen ist es wichtig, dass sie während der Gruppenarbeit die Geduld nicht verlieren, wenn die Lernenden Verschiedenes ausprobieren und zu keiner Lösung kommen. „Bedingungen, welche den Lernerfolg kurzfristig maximieren, sind nicht notwendigerweise diejenigen, welche den Lernerfolg langfristig maximieren“ schreiben Kapur & Bielaczyc (S. 78, Ãœbersetzung von mir) angesichts der weniger als 20% gelöster Einstiegsaufgaben der PS Gruppen und der 92% richtig gelöster Hausaufgaben der DI Klassen. Sogar wenn sich die Lehrpersonen zurückhalten, werden die Lernenden nach einer Lösung fragen, solange sie noch nicht gewohnt sind, auf diese Art zu arbeiten. Die Lösungen sollte man ihnen auf keinen Fall geben, sondern die Lernenden einfach ermuntern, auf möglichst viele Arten danach zu suchen.
• Auswerten der Gruppenarbeiten: Auch hier wären verschiedene Formen möglich. Beispielsweise könnte die Lehrperson die Resultate der Gruppen einsammeln und dann darauf gestützt für die nächste Woche einen Input vorbereiten. Die Diskussion in der ganzen Klasse hat den Vorteil, dass die verschiedenen Gruppen und die Lehrperson ins Gespräch kommen und gemeinsam die Stärken und Schwächen der Lösungen der einzelnen Gruppen herausarbeiten können. Die Erklärungen der Lehrperson zum „regulären“ Vorgehen können dann direkt auf diese allen präsenten Diskussionen aufsetzen.
• Begleiten der Diskussion: Die Gruppen stellen der Reihe nach ihr Vorgehen und ihre Lösungsansätze vor. Die Rolle der Lehrperson besteht einmal darin, die Diskussion zwischen den Gruppen anzuregen. Im Idealfall entsteht so ein Bild der Stärken und Schwächen der einzelnen Vorgehensweisen. Wichtig ist dabei, dass die Diskussion nicht nur Schwächen hervorhebt, sondern dass auch Stärken festgehalten werden. Es kann sein, dass eine Variante zwar keine exakte Lösung produziert, aber doch eine gute Näherung, die im aktuellen Fall sogar für praktische Zwecke genügend, gut wäre. Es kann sein, dass eine Variante nur im aktuellen Fall funktioniert, aber in anderen Fällen versagen würde. Etc.
  Wichtig ist darüber hinaus, dass all diese Stärken und Schwächen, all die Ideen und Schwierigkeiten der einzelnen Gruppen festgehalten und gewürdigt werden. Im Idealfall steht am Ende dieses Schrittes eine kleine Liste von Anforderungen an ein professionelles Vorgehen und daneben die Fragen, welche die Lösungsversuche der Gruppen offen gelassen haben. Diese Liste bildet dann den Ausgangspunkt zur Darstellung des „regulären“ Vorgehens durch die Lehrperson.
• Haltung während der Diskussionsphase: Damit die Diskussion in der notwendigen Offenheit ablaufen kann, ist wichtig, dass alle Beteiligten diese Diskussion als wichtig und notwendig wahrnehmen. Die Lehrperson kann hier viel dazu beitragen, indem sie sich echt für die Lösungsideen der einzelnen Gruppen interessiert und bereit ist, daraus auch eventuell neue Ideen zu entnehmen. Dies wird unterstützt, wenn – wie schon erwähnt – nicht nur die Schwächen sondern auch die Stärken des Vorgehens der einzelnen Gruppen diskutiert wird.

Literatur

• Gallin, P., & Ruf, U. (1990). Sprache und Mathematik in der Schule. Zürich: Verlag Lehrerinnen und Lehrer Schweiz.
• Holt, J. (2004). Aus schlauen Kindern werden Schüler. Von dem, was in der Schule verlernt wird. Weinheim: Beltz.
• Kapur, M., & Bielaczyc, K. (2012 ). Designing for Productive Failure. Journal of the Learning Sciences, 21(1), 45-83. doi: 10.1080/10508406.2011.591717