Höhlenlabyrinthe | Hansruedi Kaiser

1. Textbasierte Spiele in Höhlenlabyrinthen

Aus der Anfangszeit der Computerspiele gibt es verschiedene bekannte Spiele, die ähnlich wie unser Höhlenlabyrinth funktionieren und die als Anregung dienten. Das wohl berühmteste ist „Adventure“. Entstanden ist es bereits 1972. Details dazu, sowie spielbare Versionen zum Herunterladen finden sich auf der Colossal Cave Adventure Page.

Ein Vorläufer mit einer etwas anderen Spielidee war WUMPUS. In WUMPUS geht es darum, gewisse Höhlen zu meiden, da dort Gefahren wie bodenlose Gruben, riesige Fledermäuse oder eben der WUMPUS lauern. Die Aufgabe ist damit vergleichbar mit dem verbreiteten „Minesweeper“ Spiel. WUMPUS kann an verschiedensten Orten im Internet heruntergeladen werde.

2. Die verwendeten Labyrinthe im Bild

2.1 Ein typisches Zufallslabyrinth

Die verwendeten Zufallslabyrinthe sahen im Wesentlichen alle wie das Beispiel in Figur 1 aus. Sie bestanden aus einem knappen Dutzend Höhlen von denen jede ohne erkennbare Systematik mit zwei bis drei anderen Höhlen verbunden waren. Die Beschriftungen der Ausgänge mit Himmelsrichtungen erfolgte ebenfalls ohne erkennbare Systematik.

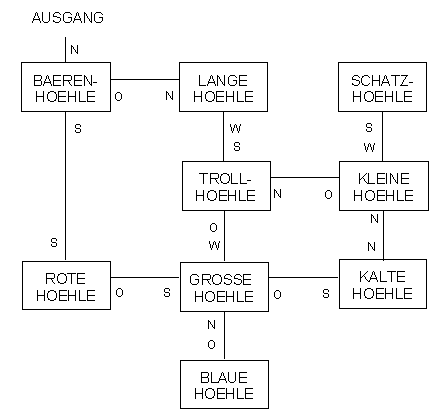
Figur 1: Ein Zufallslabyrinth

2.2 Der Aufbau rekursiver Labyrinthe an einem Beispiel

Um ein rekursives Höhlenlabyrinth aufzubauen beginnt man mit einem Grundplan, der genauso viele Höhlen enthält, wie jede Höhle Ausgänge hat (vgl. Figur 2 für ein Beispiel mit vier Ausgängen). Jede Höhle wird dann mit jeder anderen verbunden. Dabei bleibt pro Höhle ein Ausgang unverbunden. Dieser wird in allen Höhlen ausser einer (der Ausgangshöhle) gestrichen (vgl. Figur 2). Die Höhlen werden im Uhrzeigersinn durchnummeriert, beginnend mit der Ausgangshöhle. Die Ausgänge werden so angeschrieben, dass Ausgänge mit demselben Namen immer in dieselbe Höhle führen.

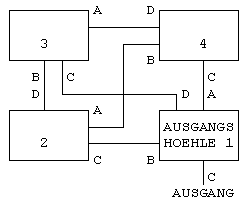
Figur 2: Grundplan einer rekursiven Höhle mit vier Ausgängen pro Höhle

Diesen Grundplan kann man nun erweitern, indem man im Grundplan jede Höhle wieder durch den Grundplan ersetzt. Für ein Labyrinth mit Höhlen die je vier Ausgänge haben sieht das dann aus wie in Figur 3. Dieses Ersetzen kann man grundsätzlich beliebig oft wiederholen (daher der Name „rekursives Labyrinth“) und erhält so beliebig grosse Höhlenlabyrinthe. Die neuen Höhlennamen werden gebildet, indem die Nummer der ersetzten Höhle mit der Nummer der neu eingesetzten Höhle kombiniert. Die Ausgänge erhalten wie in Figur 3 bei jeder Ersetzung dieselben Namen.

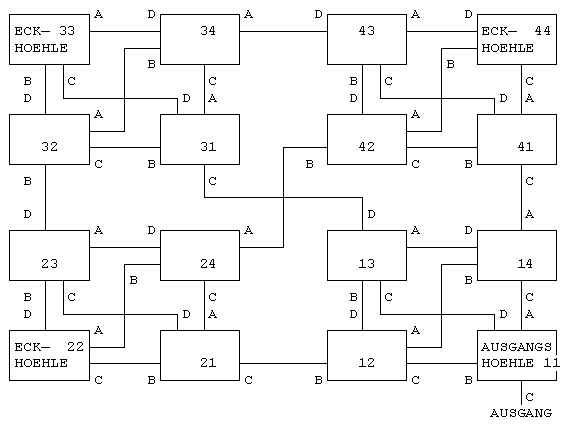
Figur 3: Rekursives Labyrinth mit vier Ausgängen pro Höhle, einmal eingesetzt

3. Empirischen Untersuchungen

3.1 Methodische Details

Natürlich wollten wir auch sehen, ob die von uns zusammengestellten und plausiblen Schwierigkeiten sich auch im Versuch mit realen Lernenden nachweisen lassen. Wir kreierten dazu noch zwei weitere Labyrinthtypen, die wir „Kubuslabyrint“ und „Palastlabyrinth“ nannten (Kaiser, H. & Unternährer, F. (1991). Verwirrliche und andere Höhlenlabyrinthe. Internes Forschungspapier. Bern, Psychologischen Instituts der Universität Bern.). Mit diesen konstruierten wir vier Aufgaben, von denen wir, wie in Tabelle 1 festgehalten, erwarteten, dass sie unterschiedlich gut „durch Tun“ bzw. „durch Instruktion“ lernbar sein würden.

Tabelle 1: Höhlenlabyrinthe die teils „durch Tun“, teils „durch Instruktion“ erlernbar sind

	Mit Instruktion	Ohne Instruktion
Zufallslabyrinth i+ t+	zu Beginn (deutlich) weniger Schritte als ohne Instruktion	(rasche) Abnahme der Anzahl Schritte von Versuchen zu Versuch
Palastlabyrinth i+ t-	zu Beginn weniger Schritte als ohne Instruktion	keine Abnahme der Anzahl Schritte von Versuch zu Versuch
Kubuslabyrinth i- t+	zu Beginn gleich viele Schritte wie ohne Instruktion	Abnahme der Anzahl Schritte von Versuch zu Versuch
Rekursives Labyrinth i- t-	zu Beginn gleich viele Schritte wie ohne Instruktion	keine Abnahme der Anzahl Schritte von Versuch zu Versuch

Der Lernerfolg wurde grob dichotom bewertet. Entweder galt „‚Lernen durch Tun’/’Lernen durch Instruktion‘ ist für dieses Höhlenlabyrinth möglich“ oder dann „‚Lernen durch Tun’/’Lernen durch Instruktion‘ ist für dieses Höhlenlabyrinth nicht möglich“.

„Lernen durch Tun“ ist möglich: Lerner können die Aufgabe „durch Tun“ innerhalb nützlicher Frist lösen und die Länge ihrer Lösungswege nimmt mit zunehmender Anzahl Versuche ab.
„Lernen durch Tun“ ist nicht möglich: Lerner können die Aufgabe „durch Tun“ entweder gar nicht lösen, oder die Länge ihrer Lösungswege nimmt nicht ab.
„Lernen durch Instruktion“ ist möglich“: Die Lernkurve der Länge der Lösungswege für Lerner, die eine Instruktion erhalten, liegt unter der Lernkurve der Lerner ohne Instruktion.
„Lernen durch Instruktion“ ist nicht möglich: Die Lernkurve der Länge der Lösungswege für Lerner, die eine Instruktion erhalten, liegt auf gleicher Höhe oder sogar über der Lernkurve der Lerner ohne Instruktion.

Als Versuchspersonen machten 39 Schülerinnen und Schüler des 9. Schuljahrs (ca. 16 Jahre alt) mit. Sie hatten jeweils ca. 75 Minuten zur Verfügung, um fünf Mal den Ausgang aus einen Labyrinth des selben Typs zu finden. 24 von ihnen erreichten in allen fünf Labyrinthen den Ausgang ins Freie).

3.2 Resultate

Wie so üblich beim erstmaligen Durchführen eines solchen Versuchs, zeigte sich, dass der Teufel im Detail steckte. Z.T. waren die Labyrinthe offensichtlich zu klein, so dass die Versuchspersonen viel zu rasch den Ausgang per Zufall fanden und sich so Lerneffekte nur schlecht nachweisen liessen. Z.T. wurde die Instruktionen wider Erwarten nicht verstanden bzw. bewusst ignoriert (eine Schülerin sagte uns, dass sie den ihr gegebenen Plan für das Zufallslabyrinth absichtlich nicht benutzt habe um die Aufgabe interessanter zu gestalten!) Entsprechend zeigten die Resultate über die Anzahl benötigter Schritte bis zum Ausgang nur tendenziell in die richtige Richtung.

Als aussagekräftiger erwies sich eine Auswertung der von den Versuchspersonen für jedes Labyrinth gezeichneten Pläne. Bei den Gruppen, die eine Instruktion erhalten hatten, untersuchten wir, ob sich in den Planzeichnungen Hinweise für oder gegen das Verständnis der Instruktion finden liessen. Für die anderen wurde geprüft, ob mit zunehmender Anzahl bearbeiteter Labyrinthe Elemente in den Plänen auffindbar waren, die auf das Verständnis fundamentaler Merkmale schliessen liessen. Zusammengefasst sind die Resultate in Tabelle 2. Abgesehen vom Kubus-Labyrinth, bei dem die Instruktion wieder Erwarten wirksam war, entsprechen sie in etwa den Erwartungen.

Tabelle 2: Resultate der Plananalyse

	Mit Instruktion		Ohne Instruktion
	V	N-V	L	N-L
Zufall	2	2*	5	*
Palast	4	1*	*	5
Kubus	5*		3	1*
Rekursiv	*	5	*	6

V: Instruktion teilweise oder ganz verstanden
N-V: Instruktion nicht verstanden
L: Eigenarten des Labyrinths ganz oder teilweise gelernt
N-L: Eigenarten des Labyrinths nicht gelernt
Nach Erwartung sollten diese Felder mit einem * nicht belegt sein.

An dieser Stelle wäre es naheliegend gewesen in einer zweiten Untersuchung mit verbesserten Aufgaben und Instruktionen sowie einer grösseren Stichprobe die erwarteten Effekte auch für die Anzahl Schritte bis zum Ausgang nachzuweisen. Aus zwei Gründen führten wir dieses Vorhaben aber nicht durch:

Einmal waren die beiden Bedingungen „erlernbar durch Tun“ und „erlernbar durch Instruktion“ sehr absolut formuliert. „Erlernbar durch Tun“ bedeutete, dass keine Hilfestellung irgend welcher Art durch den Lehrer erfolgen sollte. Und „erlernbar durch Instruktion“ meinte, dass die gesamte Hilfestellung durch den Lehrer vor dem ersten Kontakt des Lerners mit der Aufgabe zu erfolgen hat. Dies sind natürlich für reale Lernsituationen unrealistisch extreme Bedingungen. Zudem zeigte sich bei unseren Diskussionen, welche die Konstruktion der Aufgaben begleiteten, dass die meisten interessanten und z.B. schulisch relevanten Aufgaben sowieso in die Kategorie „weder durch Tun noch durch Instruktion (allein) erlernbar“ fallen würden.

Zum zweiten entspricht die Fragestellung und vor allem ihre Behandlung im Rahmen eines kontrollierten Experiments einer Haltung, die schon mehrfach in Frage gestellt wurde. Das Experiment sucht nach Wissen, das dem Lehrenden gestatten würde, Aufgaben apriori mit Sicherheit in eine der beiden Kategorien „erlernbar durch Tun“ und „erlernbar durch Instruktion“ einzuteilen. Wie unsere Erfahrungen mit den Höhlenlabyrinthen gezeigt haben, scheint dies aber grundsätzlich nicht möglich zu sein. Gewisse Probleme lassen sich offenbar einfach nicht vorhersehen. Immerhin hatten wir zur Vorbereitung der einzelnen Aufgaben insgesamt gegen ein halbes Jahr Arbeit investiert, viel mehr Zeit also, als sie z.B. einem Lehrer / einer Lehrerin zur Verfügung steht, wenn diese(r) eine Lektion vorbereitet. Wenn es uns in dieser Zeit nicht gelungen ist, z.B. eine wirksame Instruktion für den nun wirklich nicht sehr komplexen Aufbau des Zufallslabyrinths zu schreiben, dann waren wir entweder dumm – oder die Probleme, die aufgetreten sind, waren wirklich nicht vorherzusehen.

Sinnvoller scheint deshalb ein kooperativer Zugang, der die Liste der Schwierigkeiten, die bei den beiden Lernarten auftreten können als Hinweis dafür nimmt, wo die Lernenden allenfalls Hilfestellungen durch den Lehrer gebrauchen können. Vielleicht lassen sie sich auch als Hinweise darauf verwenden, ob eine Einstieg über „Tun“ oder „Instruktion“ geeigneter ist. Mit dieser geänderten Haltung stellen sich dann natürlich zwei interessante Anschlussfragen:

Was ist zu tun, wenn die Lernenden über den gewählten Einstieg die Aufgabe nicht vollständig oder gar nur ungenügend beherrschen lernen?
Wie bemerkt man überhaupt möglichst unmittelbar, dass der/die Lernende Schwierigkeiten hat, dass er/sie also während der Instruktion innerlich abschaltet oder dass sich das eigene Probieren oder Entdecken totläuft und nichts mehr bringt?